Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

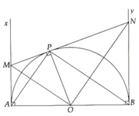
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

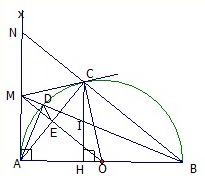
Ta có: BA, BN là tiếp tuyến (O)
⇒ OB là phân giác \(\widehat{OAN}\)
Mà △ OAN cân tại O ( vì OA = ON )
⇒ OB ⊥ AN ( đpcm )
b) Ta có: \(\widehat{MAN}=90^0\) ( vì \(\widehat{MAN}\) là góc nội tiếp chắn nửa đường tròn)
⇒ MC ⊥ AN
Mà AN ⊥ OB
⇒ MC // OB
Xét △ NMC có
MC // OB
O là trung điểm MN
⇒ OB là đường phân giác △ NMC
⇒ B là trung điểm CN

a, xét từ giác AMNC có
(Ac là tiếp tuyến của (O) ,
(MN vuông góc với CD) => \(\widehat{CAM}+\widehat{CNM}\)=180
=> AMNC nội tiếp
Xét tứ giác BMND có =90 ( BD là tiếp tuyến của (O) , \(\widehat{CND}\)=90 ( MN vuông góc với CD)
=> \(\widehat{MND}+\widehat{NAC}\)=180
=> Tứ giác BDMN nội tiếp
b, Ta có \(\widehat{CMN}=\widehat{NAC}\) (cùng chắn CN)
=> = cung AN(1)
Ta cũng có\(\widehat{NMD}+\widehat{NMD}\) (cùng chắn cung ND)
\(\widehat{NMD}\)= cung NB(2)
Từ (1) và (2) => \(\widehat{CMD}+\widehat{NMD}\)= (cung AN + cung NB)
=> \(\widehat{CMD}\)= cung AB = =90
=> tam giác CMD vuông tại M
Vì NMBD nội tiếp => \(\widehat{NDM}+\widehat{NBM}\) ( góc nội tiếp cùng chắn cung AM)
Mà \(\widehat{MCD}+\widehat{NBM}\)=90
=> \(\widehat{MCD}+\widehat{NBM}\)=90 (1)
Mặt khác \(\widehat{NAB}+\widehat{NBA}\)=90 (2)
Từ (1) và (2) => \(\widehat{MCD}=\widehat{NAB}\)
Xét tam giác ANB và CMD ta cs
\(\widehat{ANB}=\widehat{CMD}\) (=90)
\(\widehat{MCD}=\widehat{NAD}\)
=> 2 tam giác này bằng nhau

a) Xét (I) có
ΔPMN nội tiếp đường tròn(P,M,N\(\in\)(I))
MN là đường kính(gt)
Do đó: ΔPMN vuông tại P(Định lí)
mà PM=PN(P là điểm chính giữa của (I))
nên ΔPMN vuông cân tại P
\(\Leftrightarrow\widehat{PMN}=45^0\)
hay \(\widehat{SMN}=45^0\)
Xét ΔSNM vuông tại N có \(\widehat{SMN}=45^0\)(cmt)
nên ΔSNM vuông cân tại N(Dấu hiệu nhận biết tam giác vuông cân)
hay NS=NM(Hai cạnh bên)