Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ OI ⊥⊥ AB ( I ∈∈ CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=CA+DB2 =MC+MD2 =DC2 là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.
Kẻ OI \bot⊥ AB ( I \in∈ CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=\dfrac{CA+DB}{2}=\dfrac{MC+MD}{2}=\dfrac{DC}{2}IO=2CA+DB=2MC+MD=2DC là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.

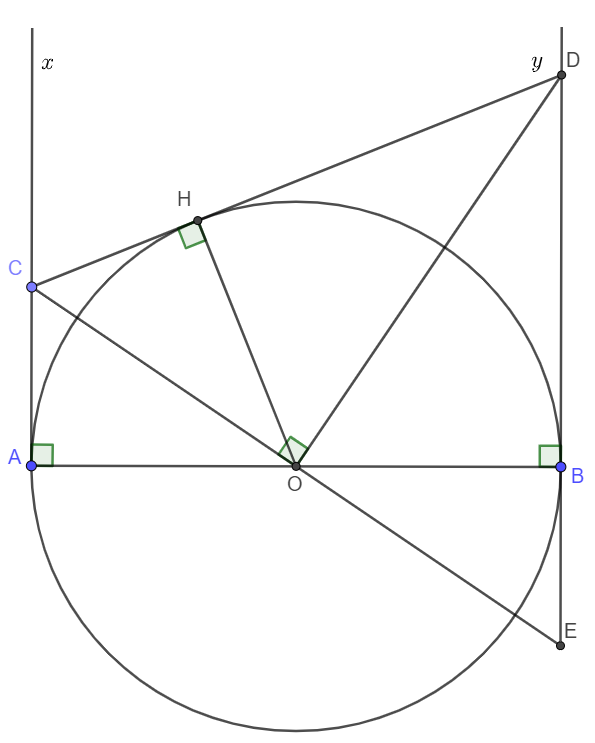
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).

O đường kính AB vẽ tiếp tuyến Ax ,By với đường tròn tâm O . Lấy E trên nửa đường tròn , qua E vẽ tiếp tuyến với đường tròn cắt Ax tại D cắt By tại C
a, Chứng minh OADE nội tiếp được đường tròn
b, Nối AC cắt BD tại F , Chung minh EFsong song với AD
Câu hỏi tương tự Đọc thêm