Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
A-B=2m^3+3m^3-4mn^2
TH1
Nếu m > n. Đặt m=n+x
óA-B=2(n+x)^3+3m^3-4(n+x)n^2
óA-B=2(n^3+3n^2x+2nx^2+x^3)=3m^3-4n^3-4n^2x
óA-B=n^3+2n^2x+6nx^2+2x^3>0
Vậy A>B
TH2
Nếu m < n. Đặt n=m+y
óA-B=2m^3+3(m+y)^3-4m(m+y)^2
óA-B=2m^3+3(m^3+3m^2y+3my^2+y^3)-4m^3-8m^2y-4my^2
óA-B=m^3+m^2y+5my^2+3y^3> 0
Vậy A > B
a) Thay m = -1 và n = 2 ta có:
3m - 2n = 3(-1) -2.2 = -3 - 4 = -7
b) Thay m = -1 và n = 2 ta được
7m + 2n - 6 = 7.(-1) + 2.2 - 6 = -7 + 4 - 6 = -9.



Ta có : n(2n - 3) - 2n(n + 1)
= 2n2 - 3n - 2n2 - 2n
= 2n2 - 2n2 - 3n - 2n
= -5n
Mà n nguyên nên -5n chia hết cho 5
a, Ta có
n(2n-3)-2n(n+1)=2n2-3n-2n2-2n
=-5n chia hết cho 5
=> DPCM
b, Ta có (2m-3)(3n-2)-(3m-2)(2n-3)
Lại có (2m-3)(3n-2)=-(3-2m)(3-2n)=(3-2m)(2n-3)
=> (2m-3)(3n-2)-(3m-2)(2n-3)=(2m-3)(3n-2)-(2m-3)(3-2n)=0
=> (2m-3)(3n-2)-(3m-2)(2n-3)=0
=>(2m-3)(3n-2)-(3m-2)(2n-3) chia hết cho 5
=> DPCM

Xét trường hợp thoy:))
Xét \(m>n\).Đặt \(m=n+k\) với \(k\in N\)
Xét \(A-B=2m^3+3n^3-4mn^2\)
\(A-B=2\left(n+k\right)^3+3n^3-4\left(n+k\right)n^2\)
\(A-B=2n^3+6n^2k+6nk^2+2k^3+3n^3-4n^3-4n^2k\)
\(A-B=n^3+2n^2k+6nk^2+2k^3>0\)
Xét \(m< n\).Đặt \(n=m+k\)
Ta có:
\(A-B=2m^3+3n^3-4mn^2\)
\(A-B=2m^3+3\left(m+k\right)^3-4m\left(m+k\right)^2\)
\(A-B=2m^3+3m^3+9m^2k+9mk^2+3k^3-4m^3-8m^2k-4mk^2\)
\(A-B=m^3+m^2k+5mk^2+3k^2>0\)
Xét \(m=n\)
Ta có:
\(A=2m^3+3n^3=2m^3+3m^3=5m^3\)
\(B=4mn^2=4mm^2=4m^3\)
\(\Rightarrow A>B\)
Vậy \(A>B\)

Ta có:
\(A-B=2m^3+3n^3-4mn^2\)
TH1: Nếu m > n. Đặt m = n + x
\(A-B=2\left(n+x\right)^3+3n^3-4\left(n+x\right)n^2\)
\(A-B=2\left(n^3+3n^2x+3nx^2+x^3\right)+3n^3-4n^3-4n^2x\)
\(A-B=2n^3+6n^2x+6nx^2+2x^3+3n^3-4n^3-4n^2x\)
\(A-B=n^3+2n^2x+6nx^2+2x^3>0\)
\(\Rightarrow A>B\)
TH2: Nếu m < n. Đặt n = m + y
Làm tương tự ra được A > B
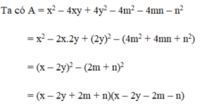
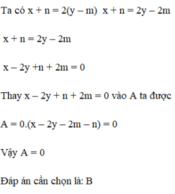
Giải:
\(A=\left(m+n\right)^3+2m^2+4mn+2n^2\)
\(\Leftrightarrow A=\left(m+n\right)^3+\left(2m^2+4mn+2n^2\right)\)
\(\Leftrightarrow A=\left(m+n\right)^3+\left(\sqrt{2}m+\sqrt{2}n\right)^2\)
\(\Leftrightarrow A=\left(m+n\right)^3+\left[\sqrt{2}\left(m+n\right)\right]^2\)
Thay \(m+n=7\) vào biểu thức A, ta được:
\(A=7^3+\left(\sqrt{2}.7\right)^2\)
\(\Leftrightarrow A=343+98\)
\(\Leftrightarrow A=441\)
Vậy \(A=441\).
Chúc bạn học tốt!!!
\(A=\left(m+n\right)^3+2m^2+4mn+2n^2\)
=\(\left(m+n\right)^3+2\left(m+n\right)^2\)
=\(7^3+2.7^2=441\)
Vậy...