CN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
DN
3 tháng 5 2018
\(7-2\sqrt{10}=5-2.\sqrt{5}.\sqrt{2}+2=\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{2}+\left(\sqrt{2}\right)^2=\left(\sqrt{5}-\sqrt{2}\right)^2\)
10 tháng 7 2021
\(\dfrac{1}{\sqrt{3}}=\dfrac{1\cdot\sqrt{3}}{\left(\sqrt{3}\right)^2}=\dfrac{\sqrt{3}}{3}\)
TT
2
KN
21 tháng 7 2019
Có: \(\sqrt{a}\sqrt{b}=\sqrt{âb}\)
\(\Rightarrow\sqrt{20}=\sqrt{4}\sqrt{5}=2\sqrt{5}\)
28 tháng 6 2021
Bởi vì ta có tính chất:
`a>=b>0=>1/a<=1/b`
GTLN bởi vì có dấu `<=`
24 tháng 11 2021
\(\sqrt{5}< \sqrt{9}=3\Leftrightarrow\sqrt{5}-3< 0\\ \Leftrightarrow\left|\sqrt{5}-3\right|=-\left(\sqrt{5}-3\right)=3-\sqrt{5}\left(đpcm\right)\)
28 tháng 5 2016
Ta có: 2m2 + 2m + 5 = 2.(m + 1/2)2 + 9/2 \(\ge\)9/2
Vì \(\left(m+\frac{1}{2}\right)^2\ge0\) nên khi cộng với \(\frac{9}{2}\)thì biểu thức sẽ \(\ge\frac{9}{2}\)
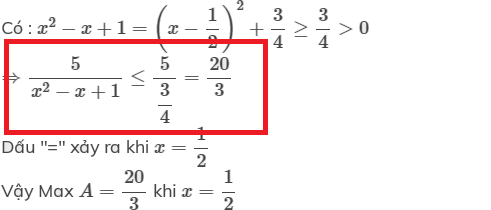
Rút gọn đi là xong :)
Ta có : \(\frac{5+\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}=\sqrt{5}+1\)
Xong !!!