Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

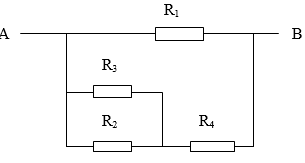
Sơ đồ mạch: R1 // [(R2 // R3) nt R4]
Điện trở tương đương là :
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{4\cdot4}{4+4}=2\left(\text{Ω }\right)\)
\(R_{234}=R_{23}+R_4=6\left(\text{Ω }\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{3\cdot6}{3+6}=2\left(\text{Ω }\right)\)

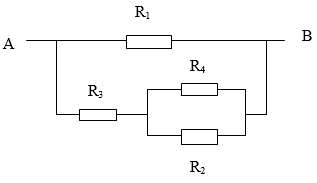
Sơ đồ mạch: R1 // [R3 nt (R2 // R4)]
\(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{234}=R_3+R_{24}=5+\dfrac{10}{3}=\dfrac{25}{3}\left(\text{Ω}\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{10\cdot\dfrac{25}{3}}{10+\dfrac{25}{3}}=\dfrac{50}{11}\left(\text{Ω}\right)\)

Hình vẽ đâu bạn. Nếu ko gửi ảnh dc thì bạn hãy viết mạch có dạng j ra nha(Vd:MCD:R1//R2 )ra nha. Chúc bạn một ngày tốt lành!

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Rightarrow R_{tđ}=3,2\left(\Omega\right)\)
\(U=U_1=U_2=U_3=2,4V\)
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{2,4}{3,2}=0,75\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{2,4}{6}=0,4\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{2,4}{12}=0,2\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{2,4}{16}=0,15\left(A\right)\end{matrix}\right.\)
1. bạn tự vẽ sơ đồ mạch điện nhé!
2.
a. \(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{16}=\dfrac{5}{16}\Rightarrow R=3,2\left(\Omega\right)\)
b. \(U=U1=U2=U3=2,4\left(V\right)\)(R1//R2//R3)
\(\left\{{}\begin{matrix}I=\dfrac{U}{R}=\dfrac{2,4}{3,2}=0,75\left(A\right)\\I1=\dfrac{U1}{R1}=\dfrac{2,4}{6}=0,4\left(A\right)\\I2=\dfrac{U2}{R2}=\dfrac{2,4}{12}=0,2\left(A\right)\\I3=\dfrac{U3}{R3}=\dfrac{2,4}{16}=0,15\left(A\right)\end{matrix}\right.\)

 không đổi; điện trở của dây dẫn và khoá không đáng kể.
không đổi; điện trở của dây dẫn và khoá không đáng kể.
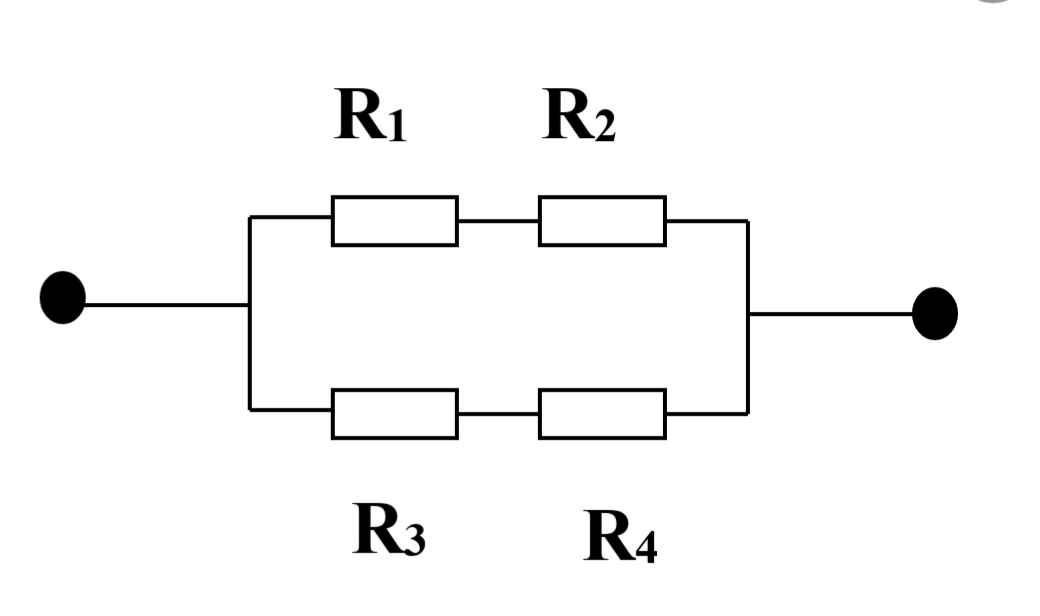
Sơ đồ mạch: R1 // [R2 nt (R3 // R4)]
\(R_{34}=\dfrac{R_3\cdot R_4}{R_3+R_4}=\dfrac{6\cdot6}{6+6}=3\left(\text{Ω}\right)\)
\(R_{234}=R_2+R_{34}=9+3=12\left(\text{Ω}\right)\)
\(R_{tđ}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{12\cdot12}{12+12}=6\left(\text{Ω}\right)\)
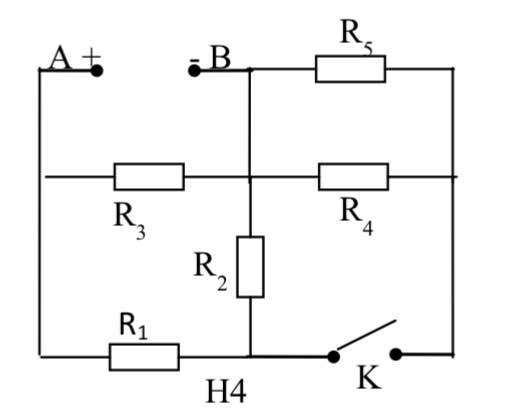
theo mạch điện như hình vẽ
\(=>\left(R1ntR3\right)//R2]ntR4\)
do đó \(=>Rtd=R4+\dfrac{\left(R1+R3\right)R2}{R1+R3+R2}\)
\(=6+\dfrac{\left(12+6\right)9}{12+6+9}=12\left(om\right)\)