Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) mạch ((R3//R4)ntR2)//R1=>Rtđ=7,5\(\Omega\)
b) R342//R1=>U324=U1=U
=>I1=\(\dfrac{U}{15}A\)
Vỉ R34ntR2=>I34=I2=\(\dfrac{U}{15}A\)
Vì R3//R4=>U3=U4=U34=I34.R34=\(\dfrac{U}{15}.5=\dfrac{U}{3}V\)=>I3=\(\dfrac{U3}{R3}=\dfrac{U}{3.10}\)
=>I4=\(\dfrac{U4}{10}=\dfrac{U}{3.10}A\)
ta có Ia=I1+I3=3A=>\(\dfrac{U}{15}+\dfrac{U}{30}=3=>U=30V\)
Thay U=30V tính được I1=2A;I2=2A;I4=1A;I3=1A
Vậy........

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

a) Điện trở tương đương đoạn mạch :
\(R = R_1 + R_2 + R_3 = 20 + 30 + 40 = 90 (\Omega) \quad\)
b) Hiệu điện thế giữa hai đầu AB :
\(U = IR = 0,2 \cdot 90 = 18 (V) \quad\)
c) Do \(R_1 \; nt \; R_2 \; nt \; R_3\) nên \(I_1 = I_2 = I_3 = I = 0,2 (A) \quad\)
Hiệu điện thế giữa hai đầu mỗi điện trở :
\(U_1 = I_1 R_1 = 0,2 \cdot 20 = 4 (V) \quad\)
\(U_2 = I_2 R_2 = 0,2 \cdot 30 = 6 (V) \quad\)
\(U_3 = I_3 R_3 = 0,2 \cdot 40 = 8 (V) \quad\)

a. \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{15.10}{15+10}=6\) (ôm)
\(\Rightarrow R_{tđ}=R_{23}+R_1=6+9=15\)(ôm)
b. Vì \(R_2\)//\(R_3\Rightarrow U_2=U_3\Leftrightarrow15I_2=10I_3\)
\(\Rightarrow I_3=\dfrac{15I_2}{10}=\dfrac{15.0,2}{10}=0,3\)(A)
\(\Rightarrow I_1=I_2+I_3=0,2+0,3=0,5\)(A)
c. ta có \(I=I_1=0,5\)
\(\Rightarrow U=I.R_{tđ}=0,5.15=7,5\)(V)
bn tự tóm tắt nhé
Giải
a,Ta có ( R2//R3)ntR1
nên Rtđ=\(\dfrac{R_2.R_3}{R_2+R_3}+R_1\)=\(\dfrac{15.100}{15+100}+9=\dfrac{507}{23}A\)
b,HĐT giữa hai đầu R2 là :
U2=I2.R2=0,2.15=3V
Ta lại có R2 //R3 =>U2=U3=3V
c đ d đ chạy qua R3 là :
I3=\(\dfrac{U_3}{R_3}=\dfrac{3}{100}=0,03A\)
=> \(I_1=I_2+I_3=0,2+0,03=0,23A\)
c, HĐT giữa 2 đầu R1,R23 là :
U1=I1.R1=0,23.9=2,07V
U23=I23.R23=0,23.\(\dfrac{15.100}{15+100}\)=\(\dfrac{39}{23}V\)
=> UAB = U1+U23=2,07+\(\dfrac{39}{23}\)\(\approx3,766V\)

bài này mình giải đk rùi. Mọi người giúp mình các bài còn lại vs. Mai mình cần lắm rùi

Bài làm:
Vì \(R_{TĐ}=0,5R_1\) nên R1 và R2 phải mắc song song
Vì \(R_1\text{/}\text{/}R_2\) nên: \(\dfrac{1}{R_{TĐ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
\(\Rightarrow R_{TĐ}=\dfrac{R_1\cdot R_2}{R_1+R_2}\Rightarrow0,5R_1=\dfrac{R_1\cdot R_2}{R_1+R_2}\)
\(\Rightarrow R_1+R_2=\dfrac{R_1\cdot R_2}{0,5R_1}\)
\(\Rightarrow R_1+R_2=2R_2\)
\(\Rightarrow R_2=R_1\)
Vậy đáp án là: D

a) Điện trở tương đương của đoạn mạch đó là Rtđ = R1 + R2 = 20 + 20 = 40 Ω.
b) Đoạn mạch mới có ba điện tích mắc nối tiếp nhau, điện trở tương đương của nó là R = R1 + R2 + R3 = 20 + 20 + 20 = 60 Ω.

 2
2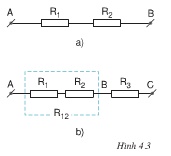
Sơ đồ mạch: R1 // [R3 nt (R2 // R4)]
\(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{234}=R_3+R_{24}=5+\dfrac{10}{3}=\dfrac{25}{3}\left(\text{Ω}\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{10\cdot\dfrac{25}{3}}{10+\dfrac{25}{3}}=\dfrac{50}{11}\left(\text{Ω}\right)\)
Rac vs Rbc đâu ạ