Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
Xét tứ giác BEDC có góc BEC=góc BDC=90 độ
nên BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng với ΔACB
=>ED/CB=AE/AC=(cos60)=1/2
=>ED=1/2CB=EM=DM
=>ΔMDE đều

Kẻ AG⊥AF
Xét △ABE và △ADG có
\(\widehat{BAE}=\widehat{DAG}\) (cùng phụ góc DAF)
\(\widehat{ABE}=\widehat{ADG}=90^o\)
suy ra △ABE=△ADG
=> AE=AG(2 cạnh tương ứng)
Xét △AGF vuông tại A đường cao AD, Ta có:
\(\dfrac{1}{AD^2}=\dfrac{1}{AG^2}+\dfrac{1}{AF^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)

Hình bạn tự vẽ nha.
a, ABCD là hình vuông \(\Rightarrow AB=BC=CD=AD\)
Ta có: \(\hat{IAD}+\hat{DAE}=90^o\)
\(\hat{BAE}+\hat{DAE}=90^o\)
\(\Rightarrow \hat{IAD} =\hat{BAE}\)
Xét \(\Delta ADI\) và \(\Delta ABE\) có:
\(\hat{ADI}=\hat{ABE}=90^o\)
\(AD=AB\left(cmt\right)\)
\(\hat{IAD}=\hat{BAE}(cmt)\)
\(\Rightarrow\Delta ADI=\Delta ABE\left(g-c-g\right)\Rightarrow AI=AE\)
b, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow AD.IK=AI.AK\) (hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow AD.IK=AE.AK\)
c, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\)(hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) mà hình vuông ABCD không đổi \(\Rightarrow\) AD không đổi\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi
Vậy \(\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi khi E thay đổi trên cạnh BC
Hai câu cuối í ẹ chưa nghĩ ra, để sau.

a) + ΔABM = ΔADN ( g.c.g )
=> AM = AN
b) + ΔANI vuông tại A, đg cao AD
\(\Rightarrow\frac{1}{AD^2}=\frac{1}{AN^2}+\frac{1}{AI^2}\) ( theo hệ thức lượng trog Δ vuông )
\(\Rightarrow\frac{1}{AB^2}=\frac{1}{AM^2}+\frac{1}{AI^2}\)
Lời giải:
a)
Xét tam giác $AND$ và $AMB$ có:
\(\widehat{ADN}=\widehat{ABM}=90^0\)
\(\widehat{DAN}=\widehat{BAM}(=90^0-\widehat{DAM})\)
\(\Rightarrow \triangle AND\sim \triangle AMB(g.g)\Rightarrow \frac{AN}{AM}=\frac{AD}{AB}=1\) (do $ABCD$ là hình vuông nên $AB=AD$)
\(\Rightarrow AM=AN\) (đpcm)
b)
Ta thấy $MC\parallel AD$ nên áp dụng định lý Ta-let:
\(\frac{AM}{AI}=\frac{CD}{DI}\Rightarrow AM=\frac{AI.CD}{DI}\)
Từ đây kết hợp với điều kiện $AB=AD=CD$ và định lý Pitago ta có:
\(\Rightarrow \frac{1}{AM^2}+\frac{1}{AI^2}=\frac{DI^2}{AI^2.CD^2}+\frac{1}{AI^2}=\frac{DI^2+CD^2}{AI^2.CD^2}=\frac{DI^2+AD^2}{AI^2.AB^2}=\frac{AI^2}{AI^2.AB^2}=\frac{1}{AB^2}\) (đpcm)

Vì ABCD là hình vuông (giả thiết).
\(\Rightarrow AB=BC=CD=DA\)(tính chất)
Và \(AB//CD\)(tính chất) \(\Rightarrow AB//DF\).
Và \(AD//CE\)(tính chất) \(\Rightarrow CE//AD\)
\(AB//DF\)(chứng minh trên)
\(\frac{AB}{AE}=\frac{FC}{FE}\)(hệ quả của định lí Ta-lét)
\(\Rightarrow\frac{AD}{AE}=\frac{FC}{FE}\)(vì \(AB=AD\))
\(\Rightarrow\frac{AD^2}{AE^2}=\frac{FC^2}{FE^2}\left(1\right)\)
Vì \(AB//CF\)(giả thiết)
\(\Rightarrow\frac{BE}{CE}=\frac{AE}{FE}\)(hệ quả của định lí Ta-lét) (2)
\(\Rightarrow\frac{BE}{CE+BE}=\frac{AE}{FE+AE}\)(tính chất của tỉ lệ thức)
\(\Rightarrow\frac{BE}{BC}=\frac{AE}{AF}\)\(\Rightarrow\frac{BE}{AD}=\frac{AE}{AF}\)(vì \(AD=BC\))
\(\Rightarrow\frac{AD}{AF}=\frac{BE}{AE}\)(tính chất của tỉ lệ thức)
Từ (2) \(\Rightarrow\frac{BE}{AE}=\frac{CE}{FE}\)(tính chất của tỉ lệ thức)
Do đó \(\frac{AD}{AF}=\frac{CE}{FE}\Rightarrow\frac{AD^2}{AF^2}=\frac{CE^2}{FE^2}\left(3\right)\)
Từ (1) và (3)
\(\Rightarrow\frac{AD^2}{AE^2}+\frac{AD^2}{AF^2}=\frac{FC^2}{FE^2}+\frac{CE^2}{FE^2}\)
\(\Rightarrow AD^2\left(\frac{1}{AE^2}+\frac{1}{AF^2}\right)=\frac{FC^2+CE^2}{FE^2}\)
Vì ABCD là hình vuông (giả thiết)
\(\Rightarrow BC\perp CD\)(tính chất)\(\Rightarrow EC\perp DF\)
Do đó \(\Delta CEF\)vuông tại C.
\(\Rightarrow CE^2+CF^2=EF^2\)(định lí Py-ta-go)
Do đó: \(AD^2\left(\frac{1}{AE^2}+\frac{1}{AF^2}\right)=\frac{FE^2}{FE^2}=1\)
\(\Rightarrow\frac{1}{AE^2}+\frac{1}{AF^2}=\frac{1}{AD^2}\)(điều phải chứng minh).
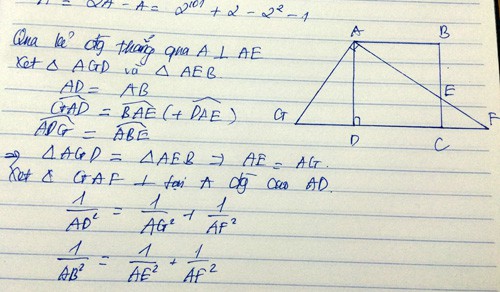
A B C D K I M
Qua đỉnh A vẽ \(AK\perp AI\).
Ta có : \(\widehat{KAD}+\widehat{DAM}=\widehat{BAM}+\widehat{MAD}=90^O\)
\(\Rightarrow\widehat{KAD}=\widehat{BAM}\)
Xét \(\Delta KADvà\Delta MAB\) lần lượt vuông tại D và B , có :
\(\left\{{}\begin{matrix}\widehat{KDA}=\widehat{ABM}=90^0\\AD=AB\left(gt\right)\\\widehat{KAD}=\widehat{BAM}\left(cmt\right)\end{matrix}\right.\)\(\Rightarrow\Delta KAD=\Delta MAB\left(cgv-gnk\right)\)
\(\Rightarrow AK=MA\)
Áp dụng hệ thức lượng vào \(\Delta AKI\) vuông tại A có :
\(\dfrac{1}{AK^2}+\dfrac{1}{AI^2}=\dfrac{1}{a^2}\)
\(\Leftrightarrow\dfrac{1}{AM^2}+\dfrac{1}{AI^2}=\dfrac{1}{a^2}\)