Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
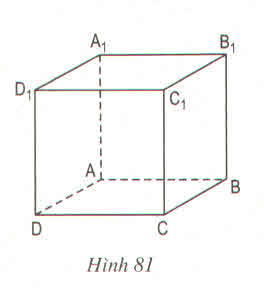
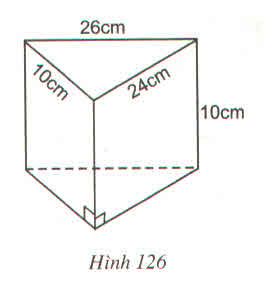
) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD
khóa vé! dúp mk nhoa nhoa! thanks các bn nhìu nha!
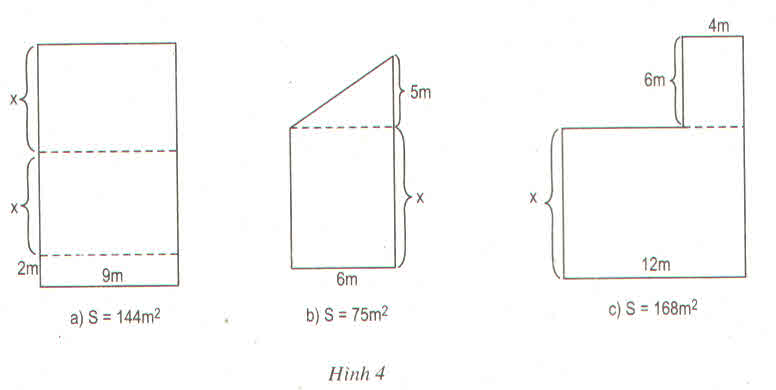
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.
a: Xét tứ giác ADCH có
M là trung điểm của AC
M là trung điểm của HD
Do đó: ADCH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
HE//AD
HE=AD
Do đó:ADHE là hình bình hành
\(\dfrac{1}{a}+\dfrac{1}{b}\ge2\sqrt[]{\dfrac{1}{ab}}\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{2}{\sqrt[]{ab}}\) (1)
Ta có \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)
\(\Leftrightarrow a-2\sqrt[]{ab}+b\ge0\)
\(\Leftrightarrow a+b\ge2\sqrt[]{ab}\)
\(\Rightarrow\dfrac{a+b}{2}\le\dfrac{2\sqrt[]{ab}}{2}\)
\(\Leftrightarrow\dfrac{a+b}{2}\le\sqrt[]{ab}\)
\(\Rightarrow\dfrac{2}{\dfrac{a+b}{2}}\le\dfrac{2}{\sqrt[]{ab}}\Leftrightarrow\dfrac{4}{a+b}\le\dfrac{2}{\sqrt[]{ab}}\) (2)
Từ (1) và (2) suy ra\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{2}{\sqrt[]{ab}}\ge\dfrac{4}{a+b}\)
hay \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
giả sử \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)(1) đúng
\(\Rightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\\ \Rightarrow\left(a+b\right)^2\ge4ab\)
\(a^2+2ab+b^2\ge4ab\)
trừ hai vế với 4ab, ta được:
\(a^2-2ab+b^2\ge0\Leftrightarrow\left(a-b\right)^2\ge0\)(2)
vì bất đẳng thức (2) luôn đúng nên bất đẳng thức (1) luôn đúng
dấu "=" xảy ra khi và chỉ khi a=b
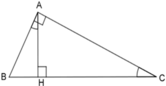
Xét 2 tam giác vuông AHB và CHA có: B A H ^ = A C H ^ (gt)
=> ΔAHB ~ ΔCHA (g - g)
=> A đúng
Xét 2 tam giác vuông AHC và BAC có:
C chung
=> ΔAHC ~ ΔBAC (g - g)
=> D đúng
Xét hai tam giác vuông BAH và BCA có:
B chung
B A H ^ = B C A ^ (gt)
=> ΔBAH ~ ΔBCA (g - g) nên B đúng, C sai.
Đáp án: C