
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. đề bạn ghi rõ lại giúp mình đc ko r mình giải lại cho
2. Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x^2}{2.3^2}=\dfrac{y^2}{5^2}=\dfrac{2x^2-y^2}{18-25}=\dfrac{-28}{-7}=4\)
\(\dfrac{x}{3}=4\Rightarrow x=12\)
\(\dfrac{y}{5}=4\Rightarrow y=20\)
Vậy x=12 và y=20

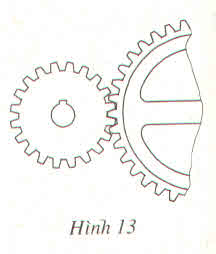
Vì số răng cưa và vận tốc là hai đại lượng tỉ lệ nghịch với nhau nên ta có:
x20=60yx20=60y hay xy = 60.20
Nên y=1200x
Vì số thời gian không đổi nên số răng cưa và số vòng quay là 2 đại lượng tỉ lệ nghịch.
\(\Rightarrow\dfrac{20}{y}=\dfrac{x}{60}\\ \Leftrightarrow xy=20.60\\ \Rightarrow xy=1200\\ \Rightarrow y=\dfrac{1200}{x}\)
Vậy \(y=\dfrac{1200}{x}\)

a)\(\frac{x}{4}=\frac{y}{5}=\frac{x.y}{4.5}=\frac{80}{20}=4\)
\(x=4\cdot4=16\\ y=5\cdot4=20\)mk ko bt cau b

Đặt: \(\frac{x}{4}=\frac{y}{5}=k\)
=> x = 4k , y = 5k
=> \(xy=4k\cdot5k=20k^2\)
=> 80 = 20k2
=> 80 : 20 = k2
=> k2 = 4 => k = 2 hoặc k = -2
Từ đó suy ra : x = -8 , y = -10 hay x = 8,y = 10
Ta có x . y = 80 => x = \(\frac{80}{y}\)
Theo đề ta có : \(\frac{x}{4}=\frac{y}{5}\)
Hay \(\frac{80}{4y}=\frac{y}{5}\)
=> 80 x 5 = 4y2
=> y2 = 100
=> y = 10 hoặc y = -10
TH1 : y = 10 thì x = 80 : 10 = 8
TH2 : y = -10 thì x = 80 : (-10) = -8

Với \(7x=3y\Rightarrow x=\frac{3y}{7}\)
Thay \(x=\frac{3y}{7}\)vào biểu thức \(3x+y=80\); ta được :
\(\frac{3y.3}{7}+y=80\Leftrightarrow9y+7y=80.7\Leftrightarrow16y=560\Leftrightarrow y=35\)
Vì \(y=35\Rightarrow x=\frac{3.35}{7}=15\)
Vậy ........
\(7x=3y\Rightarrow\frac{x}{3}=\frac{y}{7}\Rightarrow\frac{3x}{9}=\frac{y}{7}=\frac{3x+y}{9+7}=\frac{80}{16}=5\)
\(\Rightarrow x=5\cdot3=15\)
\(\Rightarrow y=5\cdot7=35\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x-y}{2-5}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=-4.2=-8\\y=-4.5=-20\end{matrix}\right.\)
\(\dfrac{x}{2}=\dfrac{y}{3}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=2k\\y=3k\end{matrix}\right.\)
\(\Rightarrow6k^2=54\Rightarrow k^2=9\Rightarrow k=\pm3\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=3.2=6\\y=3.3=9\end{matrix}\right.\\\left\{{}\begin{matrix}x=-3.2=-6\\y=-3.3=-9\end{matrix}\right.\end{matrix}\right.\)
c) \(3x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}\Rightarrow\dfrac{x^2}{25}=\dfrac{y^2}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{25}=\dfrac{y^2}{9}=\dfrac{x^2-y^2}{25-9}=\dfrac{1}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=\dfrac{1}{100}\Rightarrow x=\pm\dfrac{1}{10}\\y^2=\dfrac{1}{36}\Rightarrow y=\pm\dfrac{1}{6}\end{matrix}\right.\)
2)
\(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{15bk+3b}{15bk-3b}=\dfrac{3b\left(5k+1\right)}{3b\left(5k-1\right)}=\dfrac{5k+1}{5k-1}\)
\(\Rightarrow\dfrac{5c+3d}{5c-3d}=\dfrac{15dk+3d}{15dk-3d}=\dfrac{3d\left(5k+1\right)}{3d\left(5k-1\right)}=\dfrac{5k+1}{5k-1}\)
\(\Rightarrow\dfrac{5a+3}{5a-3b}=\dfrac{5c+3d}{5c-3d}\rightarrowđpcm\)

Giải:
Ta có: \(3x=5y\Rightarrow\frac{x}{5}=\frac{y}{3}\)
Đặt \(\frac{x}{5}=\frac{y}{3}=k\)
\(\Rightarrow x=5k;y=3k\)
Mà \(xy=60\)
\(\Rightarrow5k3k=60\)
\(\Rightarrow15k^2=60\)
\(\Rightarrow k^2=4\)
\(\Rightarrow k=\pm2\)
+) \(k=2\Rightarrow a=10;b=6\)
+) \(k=-2\Rightarrow a=-10;b=-6\)
- Nếu x, y là số dương thì:
\(D=\sqrt{\left(x-y\right)\left(x+y\right)}=\sqrt{\left(10-6\right)\left(10+6\right)}\)
\(=\sqrt{4.16}=\sqrt{64}=8\)
- Nếu x, y là số âm thì:
\(D=\sqrt{\left(x-y\right)\left(x+y\right)}=\sqrt{\left(-10+6\right)\left(-10-6\right)}\)
\(=\sqrt{\left(-4\right)\left(-16\right)}=\sqrt{64}=8\)
Vậy D = 8 khi x, y cùng dấu
Chọn đáp án C.