Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:
B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .
b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)
mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)
Vậy B ^ 1 = A ^ 3 = 135 ∘
c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)
Do đó A ^ 2 + B ^ 1 = 180 ∘
+) Vì a // b nên A ^ 1 + B ^ 2 = 180 ∘ (cặp góc trong cùng phía)
Mặt khác A ^ 1 − B ^ 2 = 70 0
⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘
+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà A ^ 1 = 125 ∘
⇒ A ^ 3 = 125 ∘
Ta có B ^ 2 = B ^ 4 (hai góc đối đỉnh) mà B ^ 2 = 55 ∘
⇒ B ^ 4 = 55 ∘
Bài 3. Cho hình 2 biết a // b và A4 = 370. a) Tính B2 . b) So sánh A1 và B1. c) Tính B3
a. \(A_4=B_2=37^0\left(slt\right)\)
b. \(A_1=B_1\left(dongvi\right)\)
c. \(B_3=180^0-B_2=180^0-37^0=143^0\left(kebu\right)\)
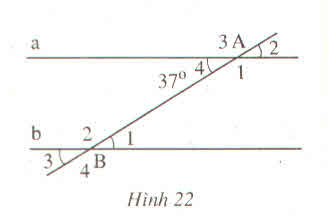
Do a // b nên ta có:
\(\widehat{A_1}=\widehat{A_3}=54^0(đối đỉnh)\)
\(\widehat{A_3}+\widehat{A_2}=180^0\)
\(\Rightarrow\)\(\widehat{A_2}=180^0-54^0=126^0\)
a)\(\widehat{B_2}=\widehat{A_3}=54^0(đồng vị)\)
b)\(\widehat{A_2}=\widehat{A_4}=126^0(đối đỉnh)\)
\(\Rightarrow\)\(\widehat{A_4}=\widehat{B_3}=126^0(đồng vị)\)
\(\widehat{A_1}<\widehat{B_3}(54^0<126^0)\)
c)\(\widehat{A_4}+\widehat{B_2}=126^0+54^0=180^0\)
a, Vì a//b và b⊥c nên a⊥c
b, Ta có \(\widehat{D_2}=\widehat{D_4}=65^0\) (đối đỉnh)
Vì a//b nên \(\widehat{C_4}=\widehat{D_2}=65^0\) (so le trong)
\(\widehat{C_3}+\widehat{C_4}=180^0\) (kề bù)
Hay \(\widehat{C_3}=180^0-65^0=115^0\)
a) Ta có: A 1 ^ + A 2 ^ + A 3 ^ = 310 ° mà A 2 ^ + A 3 ^ = 180 ° ( hai góc kề bù)
do đó A 1 ^ = 310 ° − 180 ° = 130 ° .
b) Ta có: B 2 ^ = A 2 ^ (hai góc đồng vị); B 2 ^ = B 4 ^ (hai góc đối đỉnh).
Suy ra A 2 ^ = B 4 ^