Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

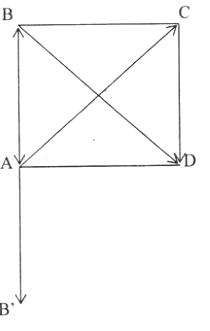
A B C D B' O
\(cos\left(\overrightarrow{AC};\overrightarrow{BA}\right)=cos\left(\overrightarrow{AC};\overrightarrow{AB'}\right)=cos\widehat{CAB'}=cos135^o\)\(=\dfrac{\sqrt{2}}{2}\).
\(sin\left(\overrightarrow{AC};\overrightarrow{BD}\right)=sin90^o=1\) do \(AC\perp BD\).
\(cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)=cos180^o=-1\) do hai véc tơ \(\overrightarrow{AB};\overrightarrow{CD}\) ngược hướng.

Đặt \(\overrightarrow{u}=\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{DC}=3.\overrightarrow{AB}+\overrightarrow{AD}\) (do \(\overrightarrow{DC}=2\overrightarrow{AB}\))
\(\Rightarrow\left|\overrightarrow{u}\right|^2=\left(3\overrightarrow{AB}+\overrightarrow{AD}\right)^2=9AB^2+AD^2+6\overrightarrow{AB}.\overrightarrow{AD}=9AB^2+AD^2=10AB^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=AB\sqrt{10}=2\sqrt{10}\)

Lời giải:
Vector cùng phương \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\)
a)
- Áp dụng định lý Pitago:
\(AC=\sqrt{AD^2+DC^2}=\sqrt{10}a\) \(\Rightarrow |\overrightarrow{AC}|=\sqrt{10}a\)
\(BC=\sqrt{BM^2+MC^2}=\sqrt{AD^2+(DC-AB)^2}=\sqrt{2}a\)\(\Rightarrow |\overrightarrow{BC}|=\sqrt{2}a\)
- \(|\overrightarrow{BM}|=|\overrightarrow {AD}|=a\)
- Áp dụng định lý Pitago cho tam giác $ADM$:
\(AM=\sqrt{AD^2+DM^2}=\sqrt{AD^2+AB^2}=\sqrt{5}a\Rightarrow |\overrightarrow{AM}|=\sqrt{5}a\)
b)
Lấy \(T\) đối xứng với \(B\) qua \(M\). Khi đó \(AMTD,BDTC\) là hình bình hành. Theo quy tắc hình bình hành:
\(2\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AD}+(\overrightarrow{AD}+\overrightarrow{AB})=\overrightarrow{AD}+\overrightarrow{AM}=\overrightarrow{AT}\)
\(\overrightarrow{BD}+\overrightarrow{BC}=\overrightarrow{BT}\)
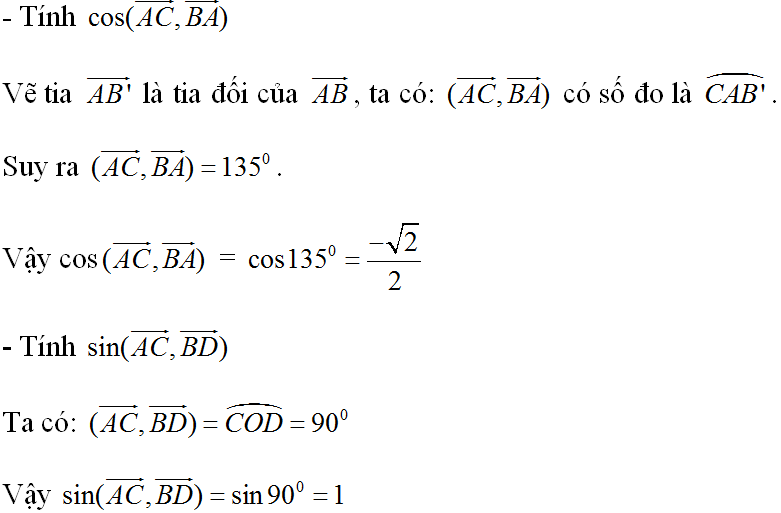
\(\widehat{A}=120^0\Rightarrow\widehat{D}=60^0\Rightarrow\left|AH\right|=\left|DH\right|.tan60^0=\frac{a\sqrt{3}}{2}\)
\(\Rightarrow\left|AD\right|=\frac{AH}{sin60^0}=a\)
\(AH.\left(CD-4AD\right)=AH.CD-4AH.AD=-4AH.AD\) (do \(AH\perp CD\))
\(=-4\left|AH\right|.\left|AD\right|.cos30^0=-4.\frac{a\sqrt{3}}{2}.a.\frac{\sqrt{3}}{2}=-3a^2\)
\(AC.BH=\left(AH+HC\right).BH=AH.BH+HC.BH\)
\(=HA.HB-HC.HB=\left|AH\right|.\left|BH\right|.cos45^0-\left|HC\right|.\left|BH\right|.cos45^0\)
Với lưu ý \(\left|HC\right|=\left|CD\right|-\left|DH\right|=\frac{3a}{2}\)
Bạn tự thay số vào tính nốt
Thankss