Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a:
xét tứ giác AEHF, ta có
góc A=90(tam giác ABC vuông tại A)
Góc E=90(E là hinh chiếu của H trên AB nên EH vuông góc với AB tại E)
Góc F=90( F là hình chiếu của H trên AC nên HF vuông góc với AC tại F)
TỪ đó suy ra tứ giác AEHF là hình chữ nhật (tứ giác có 3 góc vuông là HCN)
Câu b:
Xét tam giác ABC vuông tại A ,ta có:
AM=1/2 *BC( định ý đường trung tuyến trong tam giác vuông)
mà AM=2,5cm (gt)
suy ra BC=cm
Vì tam giác ABC vuông tại A(gt)
nên BC^2=AM^2 + AB^2(định lý pytago)
suy ra AC=4cm
xét tam giác ABC ta có:
S(ABC)=1/2(AB*AC)=1/2(3*4)=6cm vuông

Đáp án A
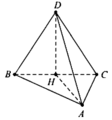
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .

Đáp án A
Gọi H là hình chiếu của S lên mặt đáy A B C suy ra S H ⊥ A B C thì H là trung điểm của AC.
Ta có:
S H = 9 − 2 = 7 ; K = P Q ∩ A B ; A B = A C = 2
Dựng P E / / A B ta có:
K B P E = Q B Q E = 1 ⇒ K B = P E = 1 3 A B = 2 3
S M N K = 1 2 d K ; M N . M N = 1 2 N B . M N = 1 2 d P ; A B C = 2 3 . S H = 2 3 7 ⇒ V P . M N K = 1 3 d P ; A B C . S M N K = 7 9
Lại có:
K Q K P = 1 2 ⇒ V Q . M N P V K . M N P = 1 2 ⇒ V Q . M N P = 1 2 V K . M N P = 7 18
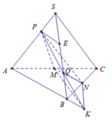

Đáp án B
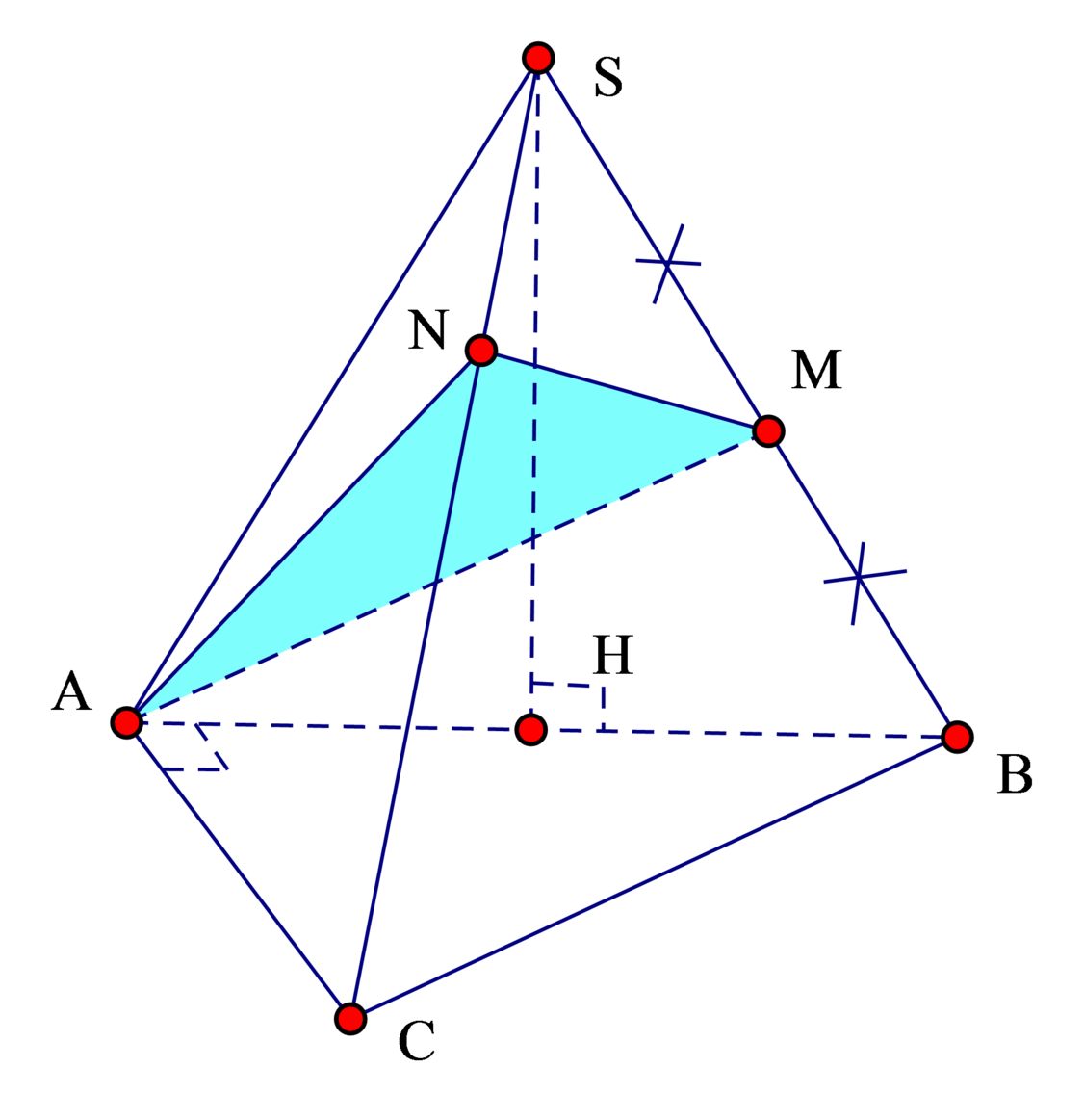
Kẻ đường cao SH trong Δ S A B ⇒ A H ⊥ A B C .
Δ S A B đều ⇒ A H = 2. a 3 2 = a 3
Diện tích tam giác: A B C = 1 2 . 2 a 2 = 2 a 2
⇒ V S . A B C = 1 3 S H . d t A B C = 1 3 a 3 .2 a 2 = 2 a 3 3 3
Ta có: V S . A M N V S . A B C = S M S B . S N S C = 1 2 . 1 3 = 1 6
⇒ V S . A M N = V S . A B C 6 = 2 a 3 3 3.6 = a 3 3 9
lớp mấy đấy