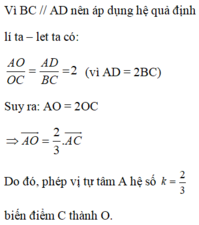Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

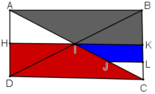
+ I là trung điểm AC; BD; HK
⇒ ĐI(H) = K ; ĐI(D) = B ; ĐI (C) = A.
⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)
+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA
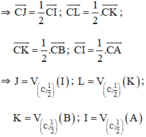
⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.
⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.
⇒ IJKI và IHDC đồng dạng.

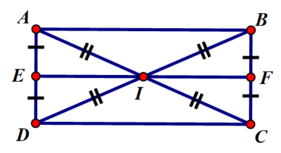
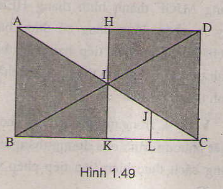
I là giao điểm AC và BD nên I là trung điểm của AC và BD
Mà AC = BD ⇒ AI = BI = 1/2 AC = 1/2 BD
Gọi E, F theo thứ tự là trung điểm của AD và BC ⇒ EF là đường trung bình của hình chữ nhật ABCD và AE = BF = 1/2 AD = 1/2 BC
⇒ EF // AB ⇒ EF vuông góc với AD và EF vuông góc với BC
Xét hai tam giác vuông AEI và BFI có:
AI = BI
AE = BF
⇒ ΔAEI = ΔBFI (cạnh huyền – cạnh góc vuông)
⇒ EI = FI (hai cạnh tương ứng)
⇒ I là trung điểm EF
Do đó, phép đối xứng qua tâm I biến hình thang AEIB thành hình thang CFID
⇒ Hai hình thang AEIB và CFID bằng nhau

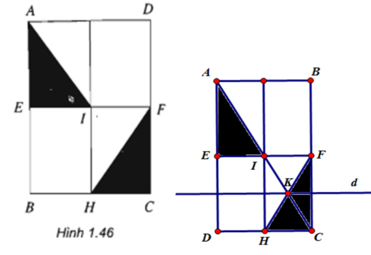
a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD

M,N lần lượt là trung điểm của SB và SB là sai đề rồi bạn. Bạn coi lại đề nha

Đ E I ( 1 ) = ( 8 ) ; T D I → ( 8 ) = ( 3 ) .
A. Phép đối xứng tâm I và phép đối xứng trục IB thì (1) không biến thành hình nào từ (2) đến (8).
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o (1) không biến thành hình nào từ (2) đến (8)
D.phép tịnh tiến theo A I → và phép đối xứng tâm I thì hình (1) thành hình (2)
Đáp án C

- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH