Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQ
Tính diện tích tam giác AMQ
SABQ / SABD = AQ / AD = 1/3 (hai tam giác chung đường cao hạ từ đỉnh B)
SABQ = SABD x 1/3 ( chú ý: SABD=1/2 SABCD)
SABQ = (216/2 ) x 1/3 = 36 (cm2)
SAMQ / SABQ = AM / AB = 1/3 (hai tam giác chung đường cao hạ từ Q)
SAMQ = SABQ x 1/3

AQ = AD - DQ = AD - \(\dfrac{3}{4}\)AD = \(\dfrac{1}{4}\)AD
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ = \(\dfrac{1}{2}\times\)\(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{4}\)AD = \(\dfrac{1}{16}\)SABCD
SBMN = \(\dfrac{1}{2}\)MB\(\times\)BN = \(\dfrac{1}{2}\)\(\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)BC = \(\dfrac{1}{8}\)SABCD
SCMN = \(\dfrac{1}{2}\)CN\(\times\)CP = \(\dfrac{1}{2}\times\dfrac{1}{2}\)BC \(\times\) \(\dfrac{2}{3}\)CD = \(\dfrac{1}{6}\)SABCD
DP = DC - CP = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC
SDPQ = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\times\)DC \(\times\) \(\dfrac{3}{4}\)AD = \(\dfrac{1}{8}\)SABCD
Diện tích của tứ giác MNPQ là:
288 \(\times\)( 1 - \(\dfrac{1}{16}\) - \(\dfrac{1}{8}-\dfrac{1}{6}-\dfrac{1}{8}\)) = 150 (cm2)
ĐS...

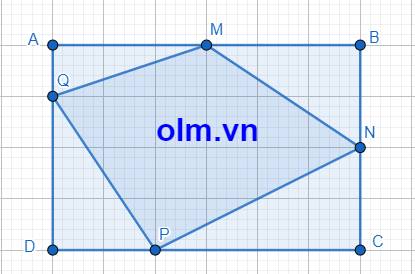
Cho hình chữ nhật ABCD có diện tích 216 cm2. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q sao cho AM = MB, BN = 2/3 BC, CP = 2/3 CD và DQ = QA. Tính diện tích hình MNPQ?

Ta thấy rằng \(\dfrac{BN}{BC}=\dfrac{AQ}{AD}\), mà \(BC=AD\) nên \(BN=AQ\), cũng có nghĩa ABNQ và CDQN là các hình chữ nhật. Ta kẻ MH và PK vuông góc với QN. Khi đó \(S_{MNPQ}=S_{MNQ}+S_{PNQ}\)
\(=\dfrac{1}{2}\times PQ\times MH+\dfrac{1}{2}\times PQ\times PK\)
\(=\dfrac{1}{2}\times PQ\times\left(MH+PK\right)\)
\(=\dfrac{1}{2}\times AB\times BC\) (do \(PQ=AB\) và \(MH+PK=BC\))
\(=\dfrac{1}{2}\times S_{ABCD}\)
\(=\dfrac{1}{2}\times324=162\left(cm^2\right)\)

SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQ
Tính diện tích tam giác AMQ
SABQ / SABD = AQ / AD = 1/3 (hai tam giác chung đường cao hạ từ đỉnh B)
SABQ = SABD x 1/3 ( chú ý: SABD=1/2 SABCD)
SABQ = (216/2 ) x 1/3 = 36 (cm2)
SAMQ / SABQ = AM / AB = 1/3 (hai tam giác chung đường cao hạ từ Q)
SAMQ = SABQ x 1/3
SAMQ = 36 x 1/3 = 12 (cm2)
Tương tự, diện tích tam giác BMN:
SBMN = 24 (cm2)
Tương tự, diện tích tam giác CNP:
SCNP = 36 (cm2)
Tương tự, diện tích tam giác DPQ:
SDPQ = 36 (cm2)
⇒ SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQ
SMNP = 216 - 12 - 24 - 36 - 36
SMNP = 108 (cm2)

SQAM = SQDP = \(\dfrac{1}{6}\) SABCD = 48 cm2
SMBN = SPNC = \(\dfrac{1}{12}\) SABCD = 24 cm2
Diện tích hình MNPQ là:
288 - (48 + 24) x 2 = 144 (cm2)
Đáp số: 144 cm2
Kẻ 2 đường chéo của MNPQ lần lượt là MP; NQ
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì BN = NC ; DQ = QA
=> Vì BC =AD=> BN = NC = DQ = QA
=> Kẻ đường chéo thứ 2 từ N sang Q = Chiều dài của hcn ABCD
=> SMNPQ = NQ*MP : 2
Mà NQ = AB và MP = BC
=> SMNPQ = AB* BC : 2
Mà AB*BC= 288
=> SMNPQ = 288 : 2
SMNPQ = 144 (cm2)

Bài này có rất nhiều lời giải tương tự chỉ thay số thôi em
Vẽ hình
Tính diện tích 4 tam giác
MNPQ = ABCD - S4 tam giác

A B C D M N P Q
Hình tớ vẽ hơi xấu, bạn thông cảm nhé.
Ta có \(S\Delta AMQ=\dfrac{1}{2}.AM.AQ=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{3}AD\)
\(=\dfrac{1}{12}.288=24\left(cm^2\right)\)
\(S\Delta MBN=\dfrac{1}{2}MB.BN=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{4}BC\)
\(=\dfrac{1}{16}.288=18\left(cm^2\right)\)
\(S\Delta QDP=\dfrac{1}{2}QD.DP=\dfrac{1}{2}.\dfrac{2}{3}AD.\dfrac{2}{3}DC\)
\(=\dfrac{2}{9}.288=64\left(cm^2\right)\)
\(S\Delta NPC=\dfrac{1}{2}.NC.CP=\dfrac{1}{2}.\dfrac{3}{4}BC.\dfrac{1}{3}.DC\)
\(=\dfrac{1}{8}.288=36\left(cm^2\right)\)
\(S_{MNPQ}=288-36-64-18-24=146\left(cm^2\right)\)
DQ + QA = DA ⇒ QA = DA - DQ = DA - \(\dfrac{2}{3}\)DA = \(\dfrac{1}{3}\)DA
SAMQ = \(\dfrac{1}{3}\)SADM( Vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)
SADM = \(\dfrac{1}{2}\)SABD(vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
SABD = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒SAMQ = \(\dfrac{1}{3}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{1}{12}\)= 24 (cm2)
SDPQ = \(\dfrac{2}{3}\)SADP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AD và DQ = \(\dfrac{2}{3}\)DA)
DP = DC - CP = DC - \(\dfrac{1}{3}\)DC = \(\dfrac{2}{3}\)DC
SADP = \(\dfrac{2}{3}\)SACD(Vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DC và DP = \(\dfrac{2}{3}\) DC)
SACD = \(\dfrac{1}{2}\)SABCD
⇒SDPQ = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\)\(\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{2}{9}\)= 64 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{4}\)BC = \(\dfrac{3}{4}\)BC
SCNP = \(\dfrac{3}{4}\)SCBP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{3}{4}\)BC)
SCBP = \(\dfrac{1}{3}\)SBCD(vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đấy CD và CP = \(\dfrac{1}{3}\) CD)
SBCD = \(\dfrac{1}{2}\)SABCD (vì ABCD là hình chữ nhật)
⇒SCNP = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) SABCD = 288 \(\times\) \(\dfrac{1}{8}\) = 36 (cm2)
SBMN = \(\dfrac{1}{4}\)SBCM (Vì hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{1}{4}\)BC)
SBCM = \(\dfrac{1}{2}\)SABC(Vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM =\(\dfrac{1}{2}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒ SBMN = \(\dfrac{1}{4}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\)\(\dfrac{1}{16}\) = 18 (cm2)
SMNPQ = SABCD - (SAMQ +SDPQ+SCNP+SBMN)
Diện tích của MNPQ là:
288 - (64 + 24 + 36 + 18) = 146 (cm2)
Đáp số: 146 cm2