Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
AK//BD
N\(\in\)BD
Do đó: AK//BN
Xét ΔMAK và ΔMBN có
\(\widehat{MAK}=\widehat{MBN}\)(hai góc so le trong, AK//BN)
MA=MB
\(\widehat{AMK}=\widehat{BMN}\)
Do đó: ΔMAK=ΔMBN
=>AK=BN
Xét tứ giác AKBN có
AK//BN
AK=BN
Do đó: AKBN là hình bình hành
b: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
mà AC cắt BD tại O
nên O là trung điểm chung của AC và BD
Xét ΔBAC có
CM,BO là các đường trung tuyến
CM cắt BO tại N
Do đó: N là trọng tâm của ΔBAC
Xét ΔABC có
N là trọng tâm của ΔBAC
CM là đường trung tuyến ứng với cạnh AB
Do đó: \(CN=2NM\)(1)
Ta có: AKBN là hình bình hành
=>AB cắt KN tại trung điểm của mỗi đường
mà M là trung điểm của AB
nên M là trung điểm của KN
=>KN=2MN(2)
Từ (1) và (2) suy ra CN=NK
mà C,N,K thẳng hàng
nên N là trung điểm của CK
c: Xét ΔBAC có
BO là đường trung tuyến ứng với cạnh AC
N là trọng tâm của ΔABC
Do đó: \(BN=\dfrac{2}{3}BO\) và \(ON=\dfrac{1}{3}BO\)
=>\(\dfrac{BN}{NO}=\dfrac{\dfrac{2}{3}BO}{\dfrac{1}{3}BO}=\dfrac{2}{3}:\dfrac{1}{3}=\dfrac{2}{3}\cdot3=2\)
=>BN=2NO
O là trung điểm của BD
=>BO=DO=BD/2
\(BN=\dfrac{2}{3}BO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BD=\dfrac{1}{3}BD\)
\(NO=\dfrac{1}{3}BO=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot BD=\dfrac{1}{6}BD\)
DO+ON=DN
=>\(\dfrac{1}{2}BD+\dfrac{1}{6}BD=DN\)
=>\(DN=\dfrac{2}{3}BD\)
\(\dfrac{DO}{DN}=\dfrac{\dfrac{1}{2}BD}{\dfrac{2}{3}BD}=\dfrac{1}{2}:\dfrac{2}{3}=\dfrac{3}{4}\)
Xét ΔDNC có OE//NC
nên \(\dfrac{DE}{DC}=\dfrac{DO}{DN}=\dfrac{3}{4}\)

a: ABCD là hình chữ nhật
=>O là trung điểm chug của AC và BD; AC=BD
=>OM=ON
Xét ΔAON và ΔCOM có
OA=OC
góc AON=góc COM
ON=OM
=>ΔAON=ΔCOM
Xet tứ giác ANCM có
O là trung điểm chung của AC và NM
=>ANCM là hình bình hành
b: Xét ΔDMC có OH//MC
nên DO/OM=DH/HC
=>DH/HC=2/1=2
=>DH=2HC
Xét ΔDOH có
N là trung điểm của DO
NE//OH
=>E là trung điểm của DH
=>DE=EH=1/2DH=HC
=>EH=1/3*DC
Xét ΔMFB và ΔMCD có
góc MFB=góc MCD
góc FMB=góc CMD
=>ΔMFB đồng dạng với ΔMCD
=>FB/CD=MB/MD=1/3
=>FB=1/3CD=EH

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
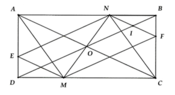
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.
Có thể vẽ hình cho em được không ạ