Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Cho hình thang ABCD có AB//CD
a: Xét ΔADC có OM//DC
nên \(\frac{AM}{AD}=\frac{AO}{AC}\left(1\right)\)
Xét ΔBAC có ON//AB
nên \(\frac{OC}{OA}=\frac{CN}{NB}\)
=>\(\frac{AO}{OC}=\frac{BN}{NC}\)
=>\(\frac{AO}{OC+OA}=\frac{BN}{BN+NC}\)
=>\(\frac{AO}{AC}=\frac{BN}{BC}\left(2\right)\)
Từ (1),(2) suy ra \(\frac{AM}{AD}=\frac{BN}{BC}\)
b: Xét tứ giác DMOE có
MO//DE
OE//MD
Do đó: DMOE là hình bình hành
=>DM=OE; DE=OM
Xét ΔADC có MO//DC
nên \(\frac{MO}{DC}=\frac{AM}{AD}\)
c: Xét ΔBDC có ON//DC
nên \(\frac{ON}{DC}=\frac{BN}{BC}\)
mà \(\frac{MO}{DC}=\frac{AM}{AD}\)
và \(\frac{BN}{BC}=\frac{AM}{AD}\)
nên OM=ON(1)
Xét tứ giác FCNO có
FC//NO
FO//NC
Do đó: FCNO là hình bình hành
=>FC=ON(2)
Từ (1),(2) suy ra FC=OM
mà OM=DE
nên FC=DE
d: Xét ΔDAB có OM//AB
nên \(\frac{OM}{AB}=\frac{DM}{DA}\)
Xét ΔADC có OM//DC
nên \(\frac{OM}{DC}=\frac{AM}{AD}\)
\(\frac{OM}{AB}+\frac{OM}{DC}=\frac{DM}{DA}+\frac{AM}{AD}=1\)
=>\(OM\left(\frac{1}{AB}+\frac{1}{DC}\right)=1\)
=>\(\frac{1}{AB}+\frac{1}{DC}=\frac{1}{OM}=\frac{2}{MN}\)

a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
b: Xét ΔDFC có
N là trung điểm của DC
NE//FC
=>E là trung điểm của DF
=>DE=EF
Xét ΔBAE có
M là trung điểm của BA
MF//AE
=>F là trung điểm của BE
=>BF=FE
=>BF=FE=ED

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
A B C D G K M F E
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
A B C M N 38 11 8
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
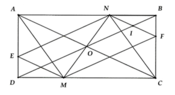
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

a: ABCD là hình chữ nhật
=>O là trung điểm chug của AC và BD; AC=BD
=>OM=ON
Xét ΔAON và ΔCOM có
OA=OC
góc AON=góc COM
ON=OM
=>ΔAON=ΔCOM
Xet tứ giác ANCM có
O là trung điểm chung của AC và NM
=>ANCM là hình bình hành
b: Xét ΔDMC có OH//MC
nên DO/OM=DH/HC
=>DH/HC=2/1=2
=>DH=2HC
Xét ΔDOH có
N là trung điểm của DO
NE//OH
=>E là trung điểm của DH
=>DE=EH=1/2DH=HC
=>EH=1/3*DC
Xét ΔMFB và ΔMCD có
góc MFB=góc MCD
góc FMB=góc CMD
=>ΔMFB đồng dạng với ΔMCD
=>FB/CD=MB/MD=1/3
=>FB=1/3CD=EH