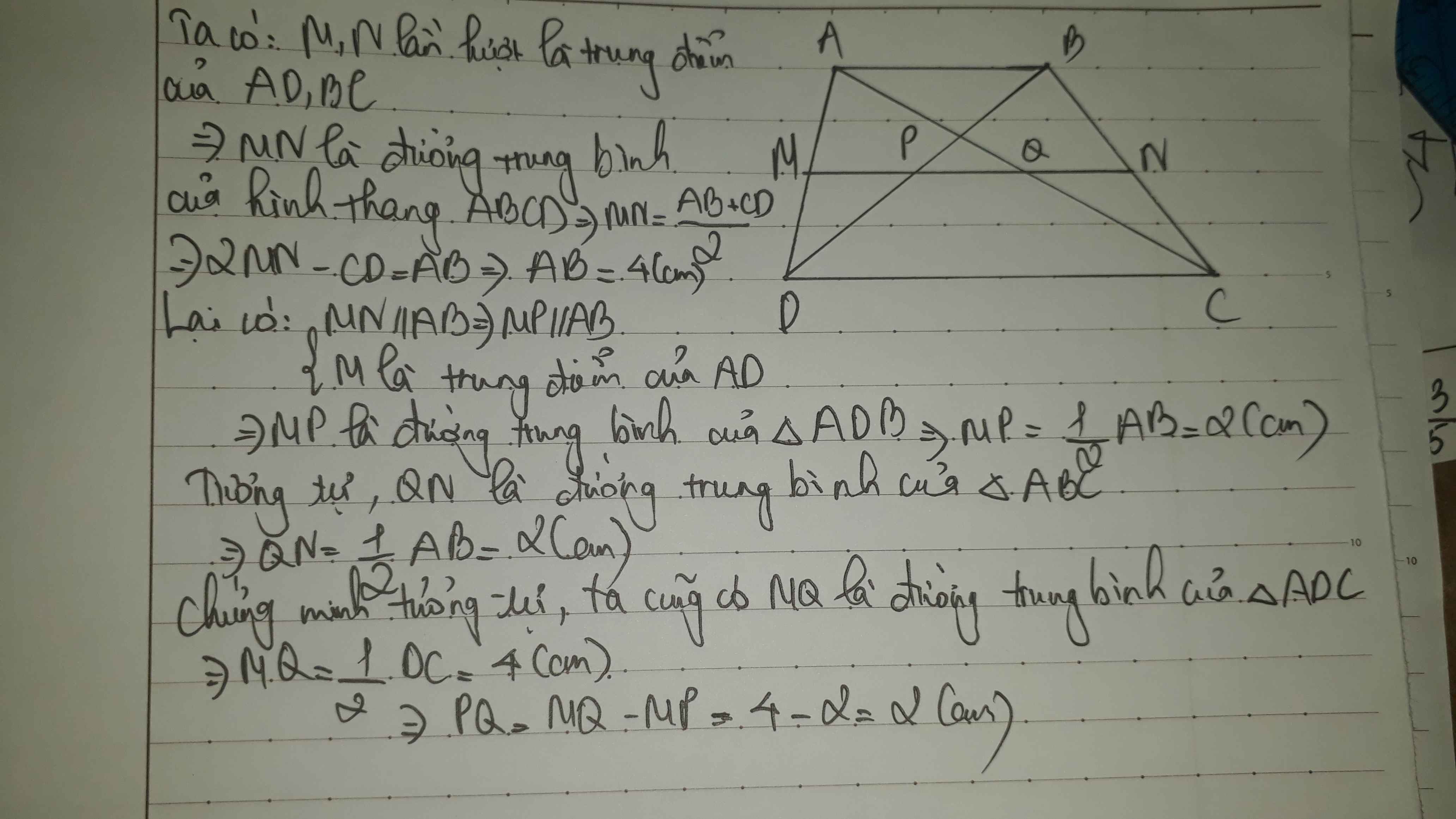Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bn tự kẻ hình nha!!
Gọi I là trung điểm của AH
Ta có IM là đg trug bình t.giác AHB
- -> IM=1/2AB và IM sog sog vs AB
- ->IMND là hình bình hành
- ->DI sog sog vs MN(1)
Do IM sog sog vs AB->IM vuông góc vs AD
Tg ADM có các đg cao AH và MI cắt nhau tại I
- -> DI vuông góc vs AM(2)
Từ (1) và (2) suy ra AM vuông góc vs MN
Tg AMN vuông tại M
Ta có :AM^2+MN^2=AN^2
Lại có:Tg ADN vuông tại D
- ->AN^2=AD^2+DN^2+AD^2/4=4^2+3^2=25
- Vậy MA^2+NM^2=25
vì sao IMND là hình bình hành vậy.
Nếu bài này ko cm như trên mà chứng minh MA vuông góc MN thì làm như nào ạ .

xét hthang ABCD có: M là t/đ của AD(gt) , N là t/đ của BC(gt)
=> MN là đg trung bình của hthang ABCD=> MN//AB//CD và MN = 1/2 . (AB+CD) (1)
xét tg ABD có: M là t/đ của AD(gt) , MI//AB (vì I thuộc MN , MN//AB) => I là t/đ của BD=> MI là đg trung bình của tg ABD
=> MI=1/2.AB => MI= 1/2.6=3(cm) (vì AB=6 cm)
c/m tương tự ta đc: KN là đg trung bình của tg ABC => KN = 1/2. AB = 1/2.6 =3 (cm) (vì AB =6cm)
Mặt khác : MN= MI +IK +KN => MN=3 +IK +3 => MN= 6+ IK (2)
Từ (1),(2) => 6+ IK = 1/2. (AB+CD)
<=> 6+IK =1/2.(6+14)
<=> 6+ IK= 10
<=> IK =4 (cm)

Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

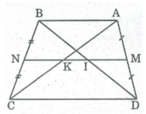
Hình thang ABCD có AB // CD
M là trung điểm của AD (gt)
N là trung điểm của BC (gt)
Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD
MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)
* Trong tam giác ADC, ta có:
M là trung điểm của AD
MK // CD
⇒ AK= KC và MK là đường trung bình của ∆ ADC.
⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)
Vậy: KN = MN – MK = 10 – 7 = 3 (cm)
* Trong ∆ ADB, ta có:
M là trung điểm của AD
MI // AB nên DI = IB
⇒ MI là đường trung bình của ∆ DAB
⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)
IK = MK – Ml = 7 – 3 = 4 (cm)