Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lớp 12 thì chúng ta tọa độ hóa cho đơn giản
Gọi O là trung điểm AB \(\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(AO=BO=\dfrac{a}{2}\)
Đặt hệ trục Oxyz vào chóp, với gốc O trùng O, tia Oz trùng tia OS, tia Ox trùng tia OB, tia Oy trùng tia ON (với N là trung điểm CD). Quy ước \(\dfrac{a}{2}\) là 1 đơn vị độ dài
Ta được tọa độ các điểm: \(S\left(0;0;\sqrt{3}\right)\) ; \(C\left(1;2;0\right)\) ; \(A\left(-1;0;0\right)\) ; \(D\left(-1;2;0\right)\)
Do M là trung điểm SD \(\Rightarrow M\left(-\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\)
\(\overrightarrow{AM}=\left(\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\) ; \(\overrightarrow{SC}=\left(1;2;-\sqrt{3}\right)\) ; \(\overrightarrow{AC}=\left(2;2;0\right)\)
\(d\left(AM;SC\right)=\dfrac{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right]\right|}=\dfrac{2\sqrt{5}}{5}=\dfrac{a\sqrt{5}}{5}\)

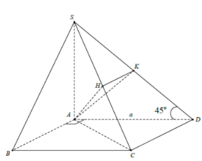
S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

Chọn B.
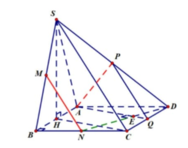
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì N D ⊥ H C N D ⊥ S H ⇒ N D ⊥ ( S H C )
⇒ N D ⊥ S C ⇒ N D ⊥ P Q
A Q → . N D → = ( A D → + D Q → ) . ( D C → + C N → ) = 0 → ⇒ A Q ⊥ N D
Vậy có
N D ⊥ P Q N D ⊥ A Q ⇒ N D ⊥ A P Q t ạ i E ⇒ d ( M N , A P ) = N E
Mà có
1 D E 2 = 1 D A 2 + 1 D Q 2 = 5 a 2 ⇒ D E = a 5
Và D N = a 5 2 ⇒ E N = 3 a 5 10
Vậy d ( M N , A P ) = 2 a 10

a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
Bạn ơi bạn chỉ mình cách bình thường được ko? Vì mình chưa học tọa độ hóa.

Chọn đáp án C
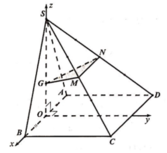
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên![]()
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: ![]()
![]()
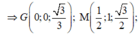
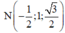
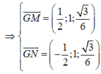
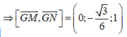
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là ![]()
Mặt phẳng (GMN) có vecto pháp tuyến là 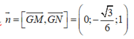
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
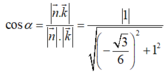
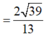

/hoi-dap/question/32725.html