Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, góc BAD=120. Mặt bên (SAB) có SA=a, SB= a\(\sqrt{3}\) và vuông góc với mặt phẳng đáy. Gọi G là trọng tâm tam giác SCD. Tính thể tích hình chóp SABCD và khoảng cách từ G đến mặt phẳng (SAB). 
S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)
S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)
Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)
Chọn A
Gọi M là trung điểm CD. Góc tạo bởi mặt bên và mặt đáy là góc SMO
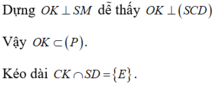
Đây là giao điểm cần tìm.
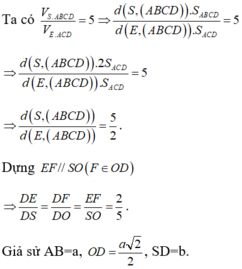
Xét tam giác vuông SOD.
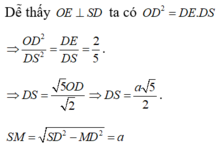
Xét tam giác vuông SOM vuông tại O có
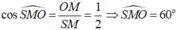
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
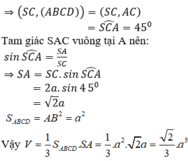
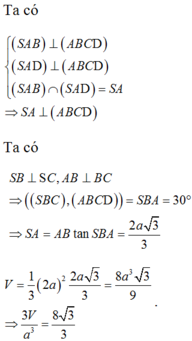
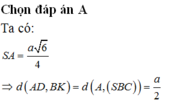
Đáp án A