Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.

Xét ΔBCD có M,N lần lượt là trung điểm của CB,CD
=>MN là đường trung bình
=>MN//BD
=>MN//(SBD)

a: ABCD là hình chữ nhật
=>CD//AB
mà AB⊂(SAB) và CD không nằm trong mp(SAB)
nên CD//(SAB)
b: ABCD là hình chữ nhật
=>BC//AD
mà AD⊂(SAD) và BC không nằm trong mp(SAD)
nên BC//(SAD)

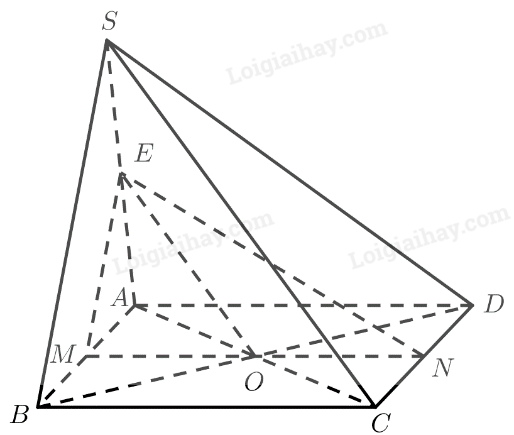
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)

a: AB//CD
Cắt nhau: AB và AC; CD và AC
b: Vì M,N lần lượt thuộc SA,SB
nên MN thuộc mp(SAB)
=>Trong 3 đoạn SA,MN,AB không có 2 đường nào chéo nhau


Ta có:MN là đường trung bình của tam giác SAB \(\Rightarrow MN//AB, MN= \frac{1}{2}AB \)
Mà \(\ CD//AB, CD= \frac{1}{2}AB \)
Suy ra: MN//CD, MN = CD.
Từ (1) và (2) suy ra MNCD là hình bình hành
Vậy NC // MD.
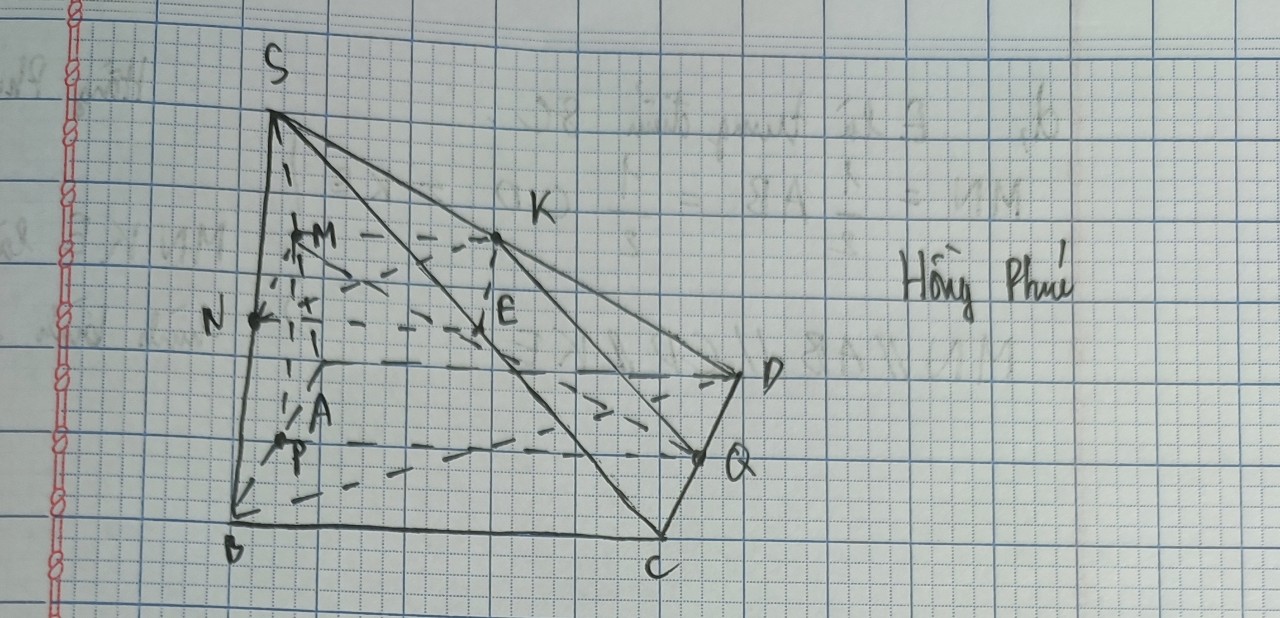
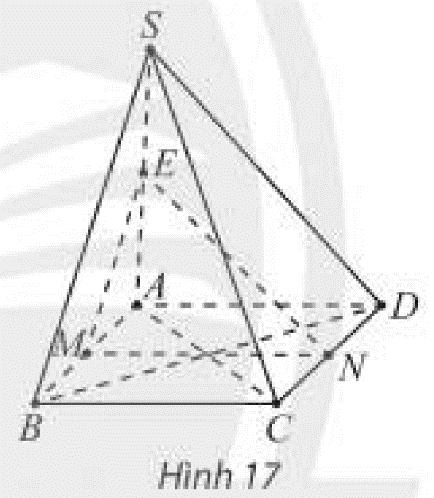
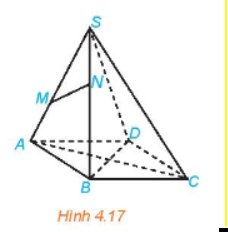
a: Xét hình thang ABCD có
M,N lần lượt là trung điểm của CD,BA
=>MN là đường trung bình
=>MN//AD//BC
=>MN//(SAD)
b:
MN//BC
\(MN\subset\left(EMN\right)\)
BC không thuộc (EMN)
Do đó: BC//(EMN)
c: AD//MN
AD không thuộc (EMN)
\(MN\subset\left(EMN\right)\)
Do đó: AD//(EMN)