Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\O\subset\left(SAC\right)\end{matrix}\right.\Rightarrow SO\subset\left(SAC\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBD\right)\\O\subset\left(SBD\right)\end{matrix}\right.\Rightarrow SO\subset\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Gọi \(K=AD\cap BC\)
\(\Rightarrow\left\{{}\begin{matrix}S\subset\left(SAD\right)\\K\subset\left(SAD\right)\end{matrix}\right.\Rightarrow SK\subset\left(SAD\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBC\right)\\K\subset\left(SBC\right)\end{matrix}\right.\Rightarrow SK\subset\left(SBC\right)\)
\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.
a: AB//CD
Cắt nhau: AB và AC; CD và AC
b: Vì M,N lần lượt thuộc SA,SB
nên MN thuộc mp(SAB)
=>Trong 3 đoạn SA,MN,AB không có 2 đường nào chéo nhau
Đáp án D
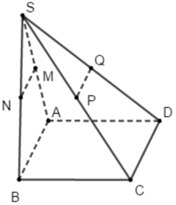
Trong tam giác SAB có M và N lần lượt trung điểm của SA và SB
Do đó MN là đường trung bình của tam giác SAB
Suy ra MN // AB
Tương tự PQ là đường trung bình của tam giác SCD
Suy ra PQ // CD
Mà ABCD là hình bình hành nên ta có AB // CD
Do đó MN // PQ // AB // CD
Vậy MN không song song với SC.
Đáp án D
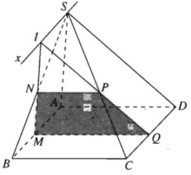
a) Vì M ∈ (SAB)
Và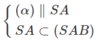 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và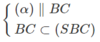 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
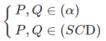⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và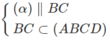 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
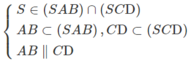⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒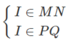 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
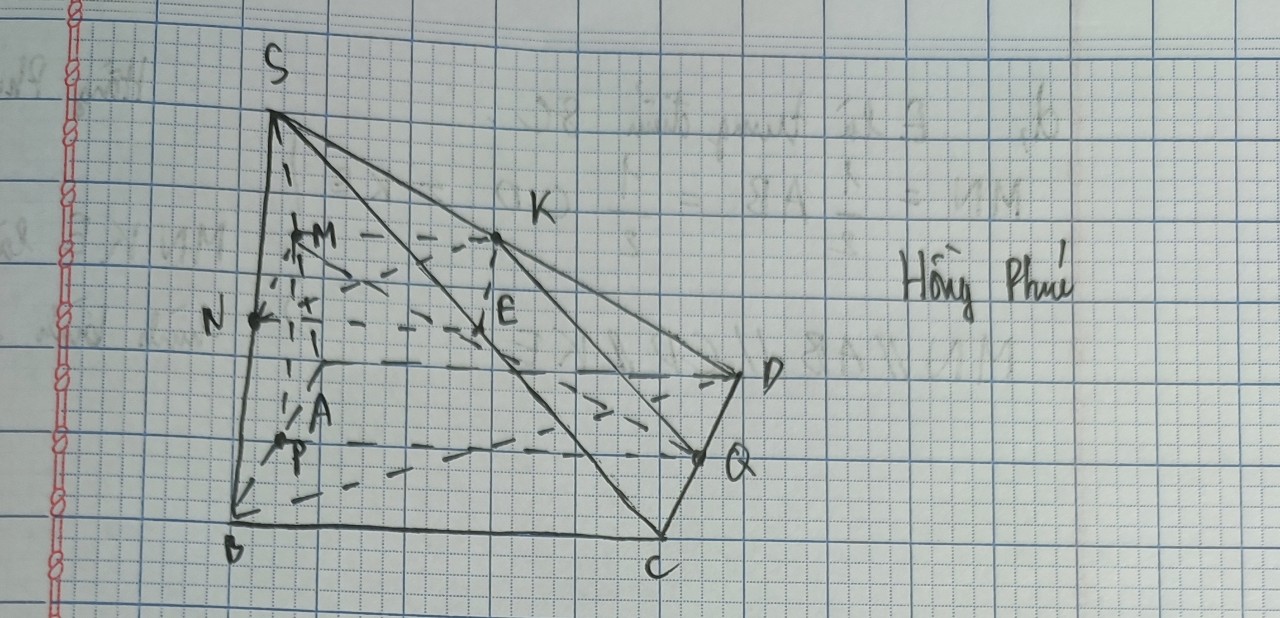
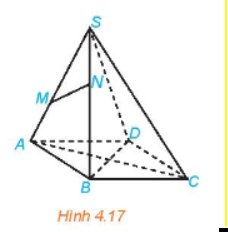
Ta có:MN là đường trung bình của tam giác SAB \(\Rightarrow MN//AB, MN= \frac{1}{2}AB \)
Mà \(\ CD//AB, CD= \frac{1}{2}AB \)
Suy ra: MN//CD, MN = CD.
Từ (1) và (2) suy ra MNCD là hình bình hành
Vậy NC // MD.