Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

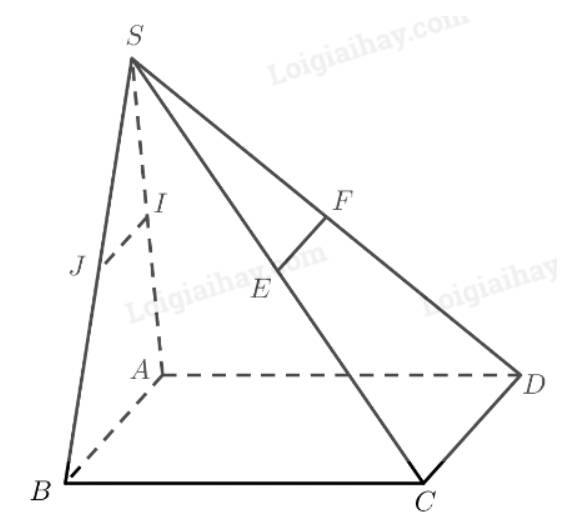
Ta có: \(I\) là trung điểm của \(SA\)
\(J\) là trung điểm của \(SB\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(SAB\)
\( \Rightarrow IJ\parallel AB\)
\(E\) là trung điểm của \(SC\)
\(F\) là trung điểm của \(SD\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(SC{\rm{D}}\)
\( \Rightarrow EF\parallel C{\rm{D}}\)
Mà \(AB\parallel C{\rm{D}}\).
Vậy \(IJ\parallel EF\parallel AB\parallel C{\rm{D}}\).
Vậy \(AD\) không song song với \(IJ\)
Chọn C.

Chọn C.
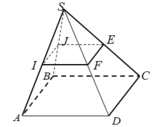
+) Ta có, IJ là đường trung bình tam giác SAB nên IJ // AB. ⇒ D đúng.
+) ABCD là hình bình hành nên AB// CD. Mà IJ// AB
Suy ra , IJ // CD ⇒ B đúng.
+) EF là đường trung bình tam giác SCD nên EF // CD.
Suy ra, IJ // EF ⇒ A. đúng.
- Do đó chọn đáp án C.

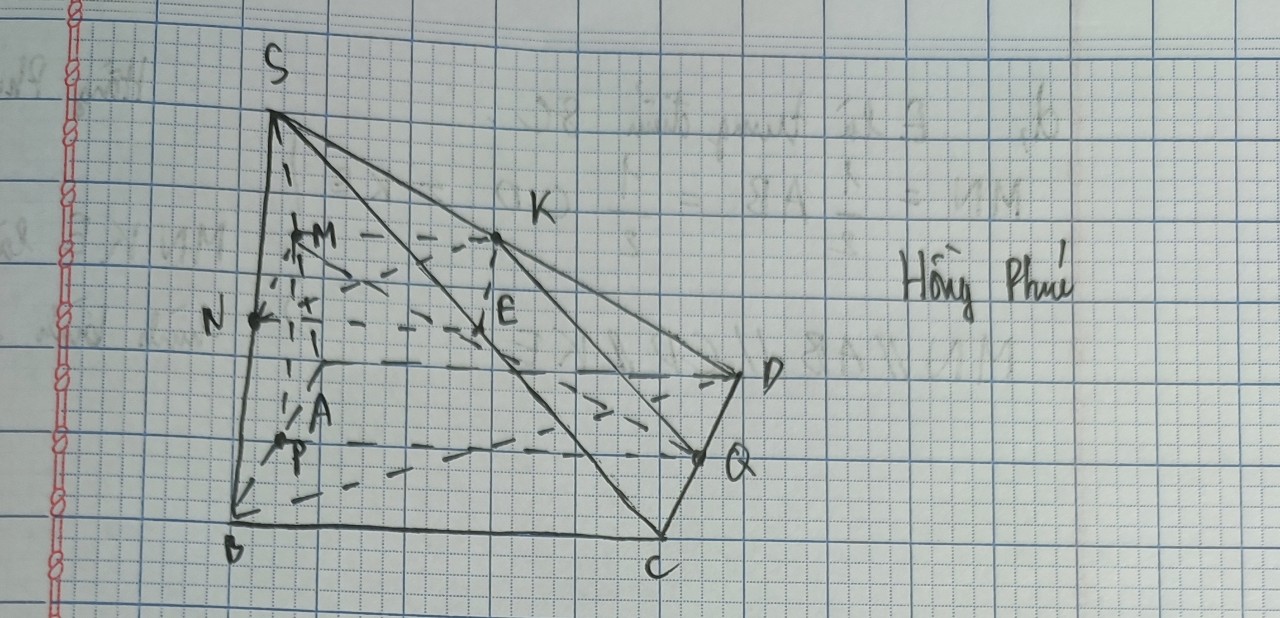
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
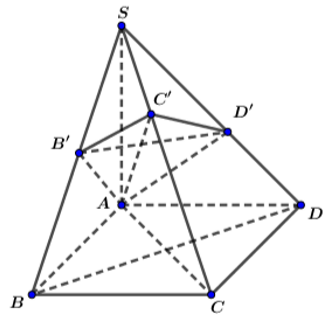
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

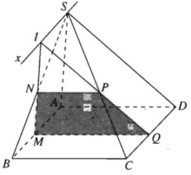
a) Vì M ∈ (SAB)
Và 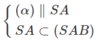 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 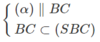 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
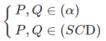 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 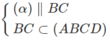 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
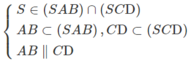 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 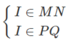
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
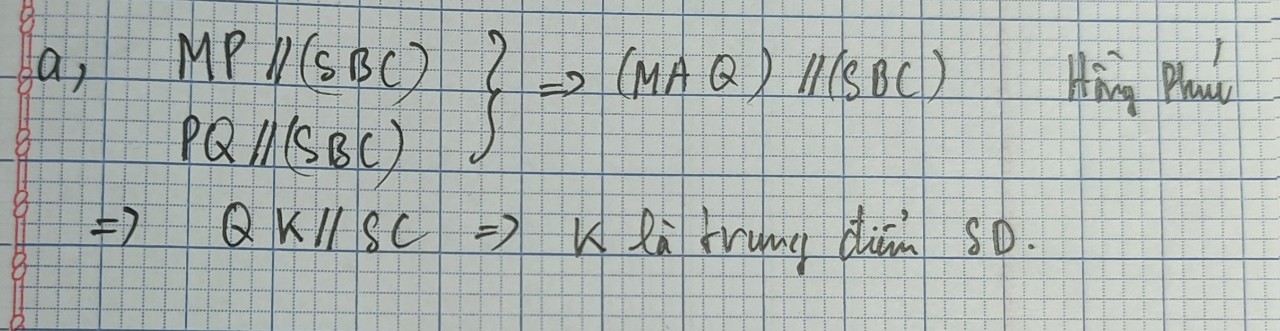




Đáp án D
Trong tam giác SAB có M và N lần lượt trung điểm của SA và SB
Do đó MN là đường trung bình của tam giác SAB
Suy ra MN // AB
Tương tự PQ là đường trung bình của tam giác SCD
Suy ra PQ // CD
Mà ABCD là hình bình hành nên ta có AB // CD
Do đó MN // PQ // AB // CD
Vậy MN không song song với SC.
Đáp án D