Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
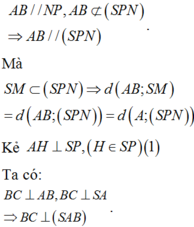
Mà
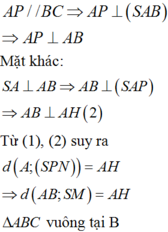
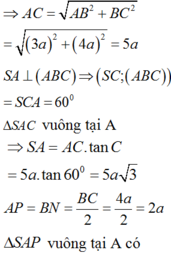
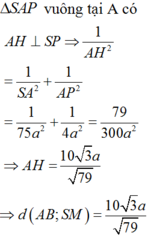
Chọn: B

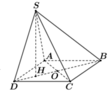
Xác định được ![]()
Tính được ![]()
![]()
Suy ra tam giác SBD vuông tại S. Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên ![]()
Chọn B.

Đáp án C

Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM//SA
![]()
=> OM là trục của đường tròn ngoại tiếp tam giác ABC,
=> OA = OB = OC
Mặt khác, tam giác SAC vuông tại A, do đó OA = OS = OC
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABC có thể tích 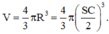
A là hình chiếu của S lên mặt phẳng (ABC), do đó góc ![]()

Chọn B
ta có: d ( I , ( S A B ) ) = 1 2 d ( C , ( S A B ) )
lại có: d ( C , ( S A B ) ) = 3 V S A B C S Δ A B C
gọi M là trung điểm AB, khi đó góc giữa mp(SAB) và mp(ABC) là góc S M H ^
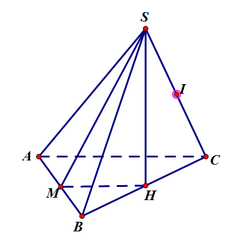
khi đó: S H = H M . tan 60 o = a 3 2
V S A B C = a 3 3 12 ; S A B C = a 2 2 ⇒ d ( C , ( S A B ) ) = a 3 2 ⇒ d ( I , ( S A B ) ) = a 3 4

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà





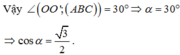

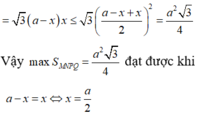
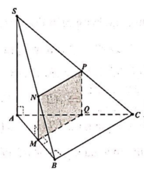


Phương pháp:
- Dựng tâm mặt cầu ngoại tiếp tứ diện.
- Xác định góc giữa OO' và mặt phẳng (ABC), chú ý tìm một đường thẳng song song với OO' suy ra góc.
Cách giải:
Gọi J là tâm đường tròn ngoại tiếp tam giác IAB.
Qua J kẻ đường thẳng vuông góc với (IAB), cắt mặt phẳng trung trực của SI tại O' thì O' là tâm mặt cầu ngoại tiếp tứ diện SIAB.
Lại có SI vừa là đường cao vừa là trung tuyến trong tam giác SCH nên tam giác SCH cân tại S