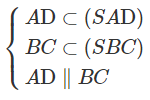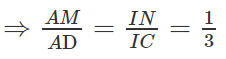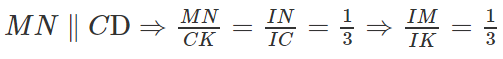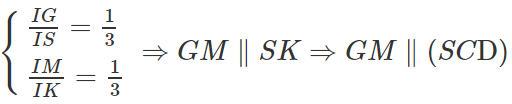Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

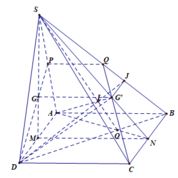
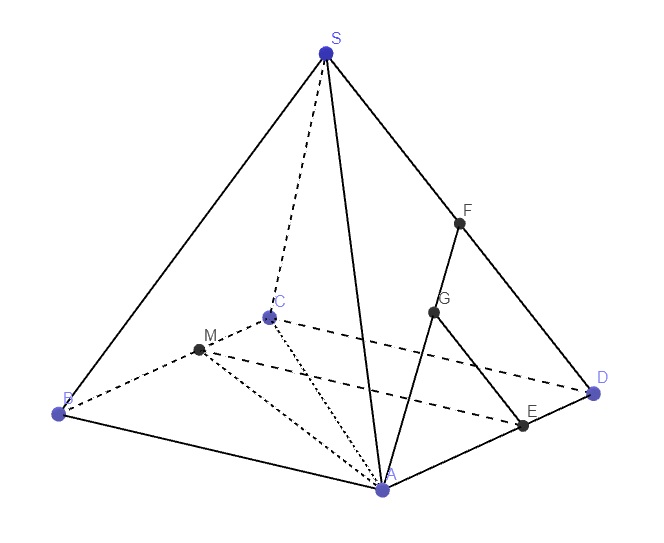
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà 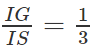
(G là trọng tâm của ∆SAB) nên
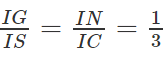
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:

Gọi F là trung điểm SD \(\Rightarrow\dfrac{GF}{GA}=\dfrac{1}{2}\) theo t/c trọng tâm
Trong mp (SAD), qua G kẻ đường thẳng song song SD cắt AD tại E
\(\Rightarrow GE||SD\Rightarrow GE||\left(SCD\right)\)
\(\left\{{}\begin{matrix}GM||\left(SCD\right)\\GE||\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow\left(GME\right)||\left(SCD\right)\Rightarrow ME||\left(SCD\right)\Rightarrow ME||CD\)
\(\Rightarrow CDEM\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow MC=ED\Rightarrow MB=EA\)
Áp dụng định lý Talet trong tam giác ADF: \(\dfrac{ED}{EA}=\dfrac{GF}{GA}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{MC}{MB}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{MAB}}{S_{MAC}}=\dfrac{MB}{MC}=2\)

Ko chắc sẽ đúng
a)* Trên mp ABCD kéo dài MN và AB sao cho MN cắt AB = { I }
Xét mp (SMN) và (SAB) có:
S là điểm chung (1)
I là điểm chung (2)
=> (SMN) n (SAB) = { SI }
* Vì I thuộc mp ABCD (cmt)
G là trọng tâm tam giác SAB
Xét mp (GMN) và (SAB) có:
G và I là điểm chung
=> (GMN) n (SAB) = {GI}