Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a b c d o e f h k
gọi o là giao của 2 đường chéo ac và bd
xét hbh abcd có 2 đường cháo ac và bd mà 2 đường chéo này lại giao nha ở o (cmt)
=> o là trung điểm của ac ; o là trung điểm của bd
xét tam giác vuông aoe và tâm giác vuông bfc
có góc aoe = góc foc (đối đỉnh )
ao=oc( o là ủng điểm của oc chứng minh rên)
-> tam giác vông aoe = tam giác vuông bfc( trường hợp cạnh huyền goác nhọn )
=> ae=cf (t/c....)
có ae=cf( cùng vuông góc với bd)
=> aecf là hình bình hành ( định nghĩa 3 : 1 cặp cạnh đối song song và = nhau)
b) tự vẽ hình nối thêm cho chính xác nhé
có abcd là hình bình hành (gt)
mà ac và bd giao tại o
-=> o là tủng điểm của ac (t/c...)
có ab//cd=> ak //hc
có ae//fc( vì aecf là hbh chứng minh câu a)=> ah // ck mà ak //ch
=> akch là hbh ( định nghĩa 1: các cặp cạnh đối song song )
có akch là hbh (cmt) có ac và hk là 2 đường chéo
o là trung điểm của ac (cmt)
=> o là tủng điểm của hk => hk đi qua o mà ac và bd cũng đi qua o (câu a)
=> hk ,ac và bd cùng đi qua o
=> hk ,bd và ac đồng quy tại o ,
ko hiểu hoặc mk sai chỗ nào ib hộ mk nhé
b: Xét ΔDKO vuông tại K và ΔBHO vuông tại H có
OD=OB
\(\widehat{DOK}=\widehat{BOH}\)
Do đó: ΔDKO=ΔBHO
Suy ra: DK=BH
Xét tứ giác BKDH có
DK//BH
DK=BH
Do đó: BKDH là hình bình hành
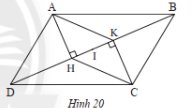
a) Vì \(AH\), \(CK\) vuông góc với \(BD\) (gt)
Suy ra \(AH\) // \(CK\)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)
\(AD = BC\) (cmt)
\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\))
Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)
Suy ra \(AH = CK\) (hai cạnh tương ứng)
Mà \(AH\) // \(CK\) (cmt)
Suy ra \(AHCK\) là hình bình hành
b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.
Mà \(I\) là trung điểm của \(HK\).
Suy ra \(I\) là trung điểm của \(AC\).
Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.
Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)
a) Xét hai tam giác vuông ADH và BCK có:
AD = BC (tính chất hình bình hành)
B1ˆ=D2ˆB1^=D2^ (slt, AB // CD)
Vậy: ΔADH=ΔBCK(ch−gn)ΔADH=ΔBCK(ch−gn)
⇒⇒ AH = CK (1)
Chứng minh tương tự ta được: ΔABK=ΔCDH(ch−gn)ΔABK=ΔCDH(ch−gn)
⇒⇒ AK = CH (2)
Từ (1) và (2) suy ra: AHCK là hình bình hành
b) O là giao điểm của AC và BD thì O là trung điểm của AC (tính chất đường chéo hình bình hành)
AHCK là hình bình hành (cmt) ⇒⇒ HK đi qua trung điểm O của đường chéo AC
Vậy H, O, K thẳng hàng.
A B D C O H K
P.s:Mìh vẽ hình hơi xấu ;))
|
Xuất sắc (100 điểm): 0 | 
Điểm hỏi đáp: 0
A B C D F K H E
a,\(\Delta AHB\&\Delta AEC\)có: \(\widehat{A}chung,\widehat{AEC}=\widehat{AHB}=90^o\)
\(\Rightarrow\Delta AHB\infty\Delta AEC\left(g.g\right)\Rightarrow\frac{AH}{AE}=\frac{AB}{AC}\Rightarrow AB.AE=AH.AC\)
b,\(\Delta AKD\&\DeltaÀFC\)CÓ: \(\widehat{A}chung,\widehat{AFC}=\widehat{AKD}=90^o\)
\(\Rightarrow\Delta AKD\infty\DeltaÀFC\left(g.g\right)\Rightarrow\frac{AK}{AF}=\frac{AD}{AC}\Rightarrow AD.AF=AK.AC\)
c, Vì ABCD là hbh => AB=DC
--------------------- => AB//CD => GÓC BAC=ACD (SO LE TRONG)
Xét tam giác ABH và tam giác CDK có:
Tam giác ABH vuông tại H
----------- CDK ------------- K
cạnh huyền AB=CD
góc nhọn BAC=ACD
=> tam giác ABH = tam giác CDK
=> AH=KC
ta có: AC = AH + HC
Mà: AH=KC
=> AC = AH+HK+AH
=> AC = AH + AK
Ta có: AB.AE+AD.AF = AH.AC+AK.AC = AC.(AH+AK) = AC.AC = AC2