
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: tổng ba góc trong một tam giác bằng 180° và \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\) nên \(\widehat {PQM} = \widehat {NMQ}\).
Xét hai tam giác MNQ và QPM có:
\(\widehat {NQM}=\widehat {PMQ}\)
MQ chung
\(\widehat {NMQ}=\widehat {PQM}\)
Vậy \(\Delta MNQ = \Delta QPM\)(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)

a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau

a: Xet ΔIMN và ΔIKN có
NM=NK
góc MNI=góc KNI
NI chung
=>ΔIMN=ΔIKN
=>góc IKN=90 độ
b:Xet ΔNKA vuông tại K và ΔNMP vuông tại M có
NK=NM
góc N chung
=>ΔNKA=ΔNMP
=>NA=NP
=>ΔNAP cân tại N
mà NI là phân giác
nên NI vuông góc PA

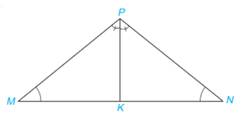
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.

a)
Xét tam giác NMD và tam giác NED, có:
NM=EH(gt)
\(\widehat{MND}=\widehat{DNE}\)(do MD là phân giác MNE)
ND là cạnh chung
Suy ra: Tam giác NMD=tam giác NED (c.g.c)
==> \(\widehat{NMD}=\widehat{NED}\) (2 góc tương ứng)
b) Có: +) MN vuông góc MP
+) EH vuông góc MP
==> MN // EH
c) Có : MN // EH
==> MNP = HEP (2 góc đồng vị)

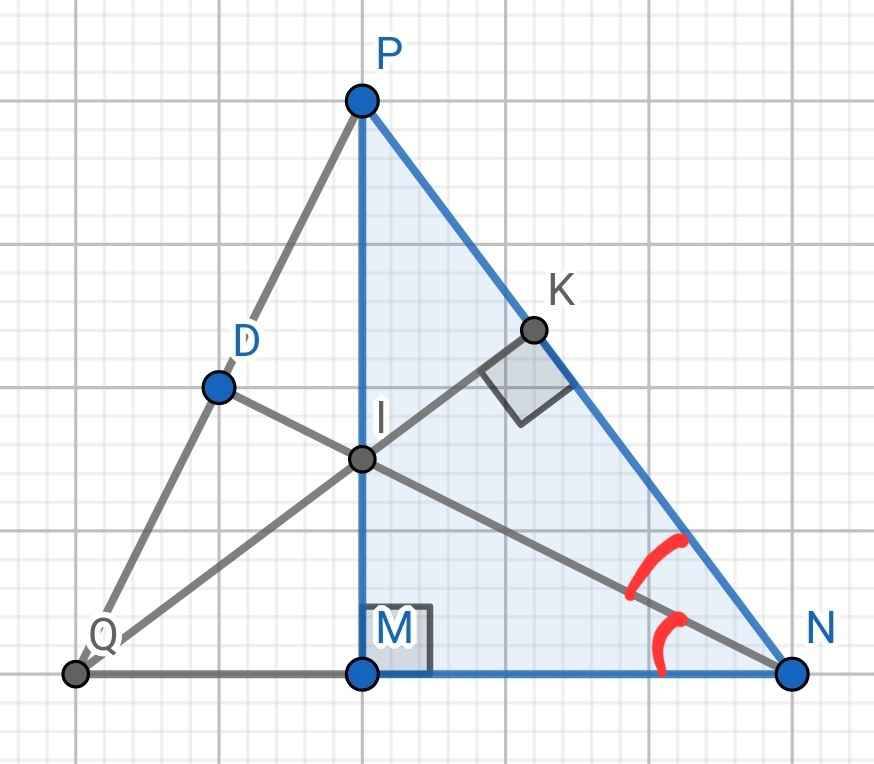
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
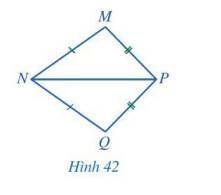
Xét tam giác MNP và tam giác QNP: MN = QN; MP = QP; NP chung.
Vậy \(\Delta MNP = \Delta QNP\) (c.c.c)
Vậy \(\widehat {MNP} = \widehat {QNP}\) ( 2 góc tương ứng)