Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có C ^ 1 + C ^ 2 = 180 0 ( 2 g ó c k ề b ù ) ;
Mà C ^ 1 = C ^ 2 nên C ^ 1 = C ^ 2 = 180 0 2 = 90 0 ;
⇒ m ⊥ a
Mặt khác a // b (có 2 góc đồng vị bằng nhau);
⇒ m ⊥ b (đpcm).


Cho hình vẽ, biết :
a) T a có: A ^ 1 = A ^ 2 = 70 0 (đối đỉnh).
Do đó A ^ 1 + B ^ = 70 0 + 110 0 = 180 0
Suy ra Ax//By (vì có cặp góc trong cùng phía bù nhau).
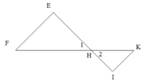
b) Ta có: F ^ = H ^ 1 ; K ^ = H ^ 2 mµ H ^ 1 = H ^ 2 ( đối đỉnh)
nên F ^ = K ^ . Suy ra EF//IK( vì có cặp góc so le trong bằng nhau).
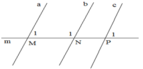
Ta có : M ^ 1 = P ^ 1 = 75 0 .
Suy ra a//c( vì có cặp góc đồng vị bằng nhau)
Ta có:
b N P ^ kÒ bï víi gãc N 1 , d o ®ã: b N P ^ = 180 0 − 105 0 = 75 0 VËy b N P ^ = P 1 ^ = 70 0
Suy ra b//c (vì có cặp góc đồng vị bằng nhau)

Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath

a: m vuông góc c
n vuông góc c
=>m//n
b: góc A1=180-75=105 độ
góc A2=180-105=75 độ
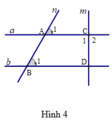
n m a b A C B D 1 1 1 2