Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

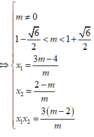

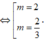

+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
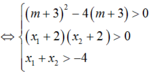
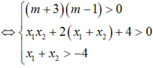
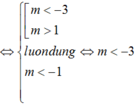
Chọn C

Lời giải:
$y'=3x^2-2(m-1)x-1$
Để hàm số có 2 điểm cực trị $x_1,x_2$ thì pt $y'=0$ có 2 nghiệm phân biệt $x_1,x_2$. Điều này xảy ra khi $\Delta'=(m-1)^2+3>0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=\frac{2(m-1)}{3}$
Khi đó:
$3(x_1+x_2)=2$
$\Leftrightarrow 2(m-1)=2$
$\Leftrightarrow m-1=1$
$\Leftrightarrow m=2$ (tm)
$\Leftright

Chọn A
![]()
Hàm số có 2 cực trị ⇔ y ' = 0 có hai nghiệm phân biệt x 1 , x 2 thỏa mãn: - 1 < x 1 < x 2
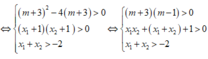
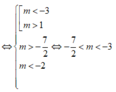

Ta có: y' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán tương đương y’ = 0 có hai nghiệm phân biệt x 1 ; x 2 t h ỏ a m ã n 4 x 1 + 3 x 2 = 3
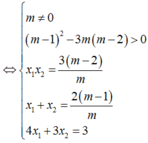
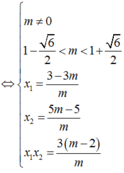
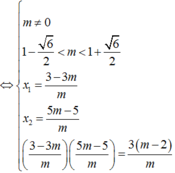
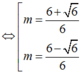
Chọn D.






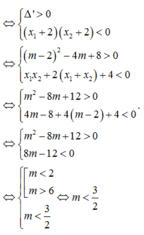
\(y'=6x^2-6\left(m+1\right)x+6m\)
\(y'=0\Leftrightarrow x^2-\left(m+1\right)x+m=0\)
\(a+b+c=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=m\end{matrix}\right.\)
\(\Rightarrow1^2+m^2=2\Rightarrow m=\pm1\)
Có 2 giá trị m nguyên thỏa mãn
Đề như vậy mà thỏa mãn 4x1^2 + x1 + x2^2 =19 thì làm sao ạ?