PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
12 tháng 1 2018
Đáp án C.
Hàm số liên tục nếu:
lim x → − 2 + f x = lim x → − 2 − f x = f 2 ⇔ 3. − 2 − 5 = − 2 a − 1 ⇔ a = 5.
PT
1
CM
4 tháng 4 2018
Đáp án D
để hàm số liên tục tại x = 1 thì
lim x → 1 + 1000 x − 1 + x − 2 x 2 − 1 = 2 a ⇒ a = 3 ln 10 + 1 4
PT
1
CM
16 tháng 6 2019
Đáp án C
Ta có: lim x → 1 − f x = lim x → 1 − x 2 2 = 1 2
lim x → 1 + f x = lim x → 1 + a x + 1 = a + 1 , f 1 = 1 2
Hàm số liên tục tại x = 1
⇔ lim x → 1 − f ( x ) = f ( 1 ) = lim x → 1 + f ( x ) ⇒ a + 1 = 1 2 ⇔ a = − 1 2
CM
23 tháng 8 2017
Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.
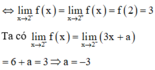
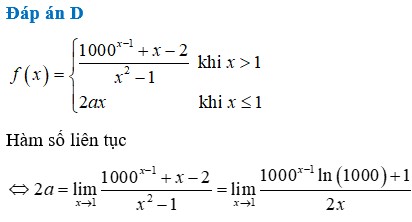
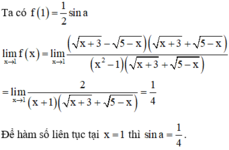
Đáp án C
Ta có
lim x → 1 + f x = lim x → 1 − f x ⇔ lim x → 1 + f a x + 1 = lim x → 1 − x 2 2 ⇔ a + 1 = 1 2 ⇔ a = − 1 2 .