Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(A\left(x;0\right)\) là giao điểm của (d1) và (d2) trên trục Ox
\(\Rightarrow\)\(A\left(x;0\right)\) là nghiệm của hệ\(\left\{{}\begin{matrix}y=2mx+m+1\left(d_1\right)\\y=\left(m-1\right)x+3\left(d_2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}0=2mx+m+1\left(d_1\right)\\0=\left(m-1\right)x+3\left(d_2\right)\end{matrix}\right.\)
Dễ thấy tại \(\left(d_2\right)\) thì \(m\ne1\) (vì nếu m=0 thì khi đó 0=3 vô lý)
Hệ\(\Leftrightarrow\left\{{}\begin{matrix}0=2mx+m+1\\x=\dfrac{3}{1-m}\end{matrix}\right.\)\(\Rightarrow2m.\dfrac{3}{1-m}+m+1=0\)
\(\Leftrightarrow-m^2+6m+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=3+\sqrt{10}\\m=3-\sqrt{10}\end{matrix}\right.\)(thỏa)
Vậy...

a) Để d1 trùng d2 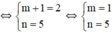
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 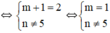
Vậy m = 1, n ≠ 5.

a) Để d1 trùng d2 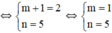
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 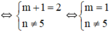
Vậy m = 1, n ≠ 5.

\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)

(a) \(\left(d_1\right)\left|\right|\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}2-m^2=-2\\-m-5\ne2m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-3\end{matrix}\right.\)
\(\Rightarrow m=\pm2.\)
(b) Viết lại phương trình đường thẳng \(\left(d_2\right)\) thành \(\left(d_2\right):y=\left(m-1\right)x+m\).
\(\left(d_1\right)\left|\right|\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}2m+1=m-1\\-\left(2m+3\right)\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-2\\m\ne-1\end{matrix}\right.\)
\(\Rightarrow m=-2.\)
(c) Phương trình hoành độ giao điểm của \(\left(d_1\right),\left(d_2\right):\)
\(m^2x+1-4m=-\dfrac{1}{4}x+1\)
\(\Leftrightarrow\left(m^2+\dfrac{1}{4}\right)x=4m\Leftrightarrow x=\dfrac{4m}{m^2+\dfrac{1}{4}}=\dfrac{16m}{4m^2+1}\).
Thay vào \(\left(d_2\right)\Rightarrow y=-\dfrac{1}{4}\cdot\dfrac{16m}{4m^2+1}+1=-\dfrac{4m}{4m^2+1}+1\).
Do hai đường thẳng cắt nhau tại một điểm nằm trên trục hoành \(\Rightarrow y=-\dfrac{4m}{4m^2+1}+1=0\)
\(\Leftrightarrow m=\dfrac{1}{2}\).

Hai đồ thị song song khi:
\(\left\{{}\begin{matrix}2m+3=m\\4\ne5\end{matrix}\right.\) \(\Rightarrow m=-3\)

a)\(\left(d1\right)\) và \(\left(d2\right)\)cắt nhau
\(\Leftrightarrow\hept{\begin{cases}5-k\ne k\\m-2=4-m\end{cases}}\Leftrightarrow\hept{\begin{cases}5=k+k\\m+m=4+2\end{cases}}\Leftrightarrow\hept{\begin{cases}2k\ne5\\2m=6\end{cases}}\Leftrightarrow\hept{\begin{cases}k\ne\frac{5}{2}\\m=3\end{cases}}\) \(\Leftrightarrow m=3\)
b) \(\left(d1\right)\)và \(\left(d2\right)\)song song khi
\(\Leftrightarrow\hept{\begin{cases}5-k=k\\m-2\ne4-m\end{cases}}\Leftrightarrow\hept{\begin{cases}k=\frac{5}{2}\\m\ne3\end{cases}}\)
c) \(\left(d1\right)\)và \(\left(d2\right)\)trùng nhau
\(\Leftrightarrow\hept{\begin{cases}5-k=k\\m-2=4-m\end{cases}}\Leftrightarrow\hept{\begin{cases}k=\frac{5}{2}\\m=3\end{cases}}\)

a) \(\left(d_1\right):y=mx+2m\)
\((d_1)\parallel (d_2)\) \(\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Rightarrow m=3\)
b) \(\left(d_1\right)\equiv\left(d_2\right)\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m=1\end{matrix}\right.\Rightarrow\) không có m thỏa
c) \(\left(d_1\right)\bot\left(d_2\right)\Rightarrow m.\left(2m-3\right)=-1\Rightarrow2m^2-3m+1=0\)
\(\Rightarrow\left(m-1\right)\left(2m-1\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)
Ta có: (d1): y=m(x+2)
nên y=mx+2m
a) Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2m=-3\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Leftrightarrow m=3\)
\(d_1//d_2\Leftrightarrow\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m-1=2m\\5\ne-4\end{cases}}\Leftrightarrow\hept{\begin{cases}-1=2m-m\\5\ne-4\end{cases}}\Leftrightarrow\hept{\begin{cases}m=-1\\5\ne-4\end{cases}}\)