Cho hai hàm số y = a x và y = log b x có đồ thị...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

25 tháng 12 2017

Cho hai hàm số y = a x và y = log b x có đồ thị như hình vẽ. Khẳng định nào dưới đây là đúng?

A. a; b > 1

B. 0 <a; b < 1

C. 0 < a < 1 <b

D. 0 < b < 1 < a

#Toán lớp 12

1

CM

Cao Minh Tâm

25 tháng 12 2017

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

15 tháng 4 2017

Cho a > 0 , b > 0 , a ≠ 1 , b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng? A. a > 1 ; 0 < b < 1. B. 0 < a < 1 ; b > 1. C. 0 < a < 1 ; 0 < b < 1. ...

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 4 2017

PT

Pham Trong Bach

17 tháng 5 2017

Cho a là số thực tùy ý và b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số y = x a , y = log b x , y = log c x , x > 0 . Khẳng định nào sau đây đúng? A. a < c < b B. a > c > b C. a > b > c D. a < b < c ...

#Toán lớp 12

1

CM

Cao Minh Tâm

17 tháng 5 2017

Chọn: D

PT

Pham Trong Bach

13 tháng 10 2017

Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị hàm y = f’(x) như hình vẽ dưới đây. Khẳng định nào trong các phương án A, B, C, D dưới đây là đúng? A. . B. . C. ....

#Toán lớp 12

1

CM

Cao Minh Tâm

13 tháng 10 2017

PT

Pham Trong Bach

2 tháng 8 2019

Cho a,b,c dương và khác 1. Các hàm số y = log a x , log b x , log c x có đồ thị như hình vẽ Khẳng định nào dưới đây đúng? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

2 tháng 8 2019

PT

Pham Trong Bach

17 tháng 8 2017

Cho hàm số y = a x 3 + b x 2 + c x + d (a,b,c,d là các hằng số,a ≠ 0) có đồ thị như sau: Khẳng định nào sau đây là khẳng định đúng? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

17 tháng 8 2017

Chọn C

PT

Pham Trong Bach

18 tháng 1 2018

Cho a > 0, b > 0, b ≠ 1 Đồ thị các hàm số y = a x và y = log b x cho như hình vẽ bên. Mệnh đề nào sau đây là đúng? A. a > 1, 0 < b < 1 B. 1 > a > 0, b > 1 C. 0 < a < 1, 0 < b < 1 D. a > 1, b >...

#Toán lớp 12

1

CM

Cao Minh Tâm

18 tháng 1 2018

PT

Pham Trong Bach

4 tháng 1 2017

Hình bên là đồ thị của ba hàm số y = a x , y = b x , y = c x ( 0 < a , b , c ≠ 1 ) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?đà A. b > a > c B. a > b > c C. a > c > b D. c > b >...

#Toán lớp 12

1

CM

Cao Minh Tâm

4 tháng 1 2017

Do y = ax và y = bx là hai hàm đồng biến nên a > 1; b > 1.

Do y = cx nghịch biến nên c < 1. Vậy c bé nhất.

Mặt khác: Lấy x = m, khi đó tồn tại y1; y2 > 0 để

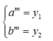
Dễ thấy y1 < y2 ⇒ am < bm ⇒ a < b

Vậy b > a > c.

Chọn A

PT

Pham Trong Bach

10 tháng 2 2017

Cho các hàm số y = log a x , y = log b x v à y = c x (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng? A. c > b > a B. c > a > b C. a > b > c D. b > a >...

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 2 2017

Đáp án D

Cách giải:

Ta thấy, hai hàm số y = logax, y = logb⁡x đều đồng biến trên (0;+∞) ⇒ a, b > 1

Lấy x0 > 0 bất kì, ta thấy logax0 > logbx0 ⇒ a < b ⇒ 1 < a < b

Hàm số y = cx nghịch biến trên R ⇒ c < 1 ⇒ c < a < b

PT

Pham Trong Bach

11 tháng 9 2018

Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x = c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b. Khẳng định nào sau đây là khẳng định đúng? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

11 tháng 9 2018

Chọn D

Ta có

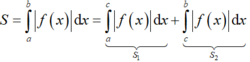
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).

Do đó, S 1 = - ∫ a c f x d x .

Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).

Do đó, S 2 = ∫ c b f x d x .

Vậy S = - ∫ a c f x d x + ∫ c b f x d x .

PT

Pham Trong Bach

8 tháng 10 2019

Cho 3 số a, b, c > 0, a ≠ 1 ; b ≠ 1 ; c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , y = c x được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 10 2019