Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn C 1 có tâm I 1 1 ; 2 và bán kính R 1 = 1 .
Đường tròn C 2 có tâm I 2 - 1 ; 0 và bán kính R 2 = 1 .

Chọn B

Chọn A
Ta có ![]() và
và 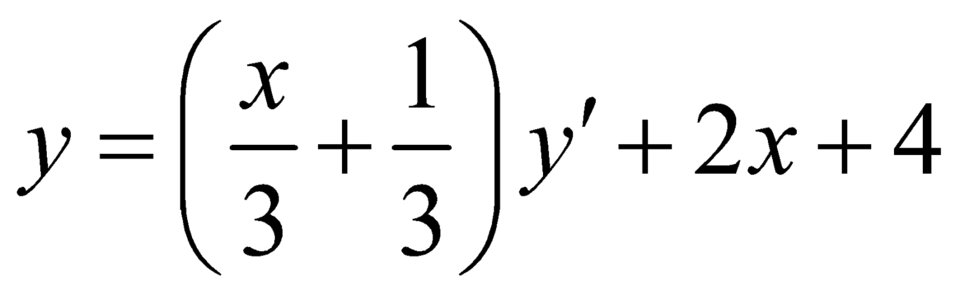 ,
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là ![]() ,
, ![]() .
.
Đường tròn ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]() .
.
Đường thẳng ![]() tiếp xúc với đường tròn
tiếp xúc với đường tròn ![]() khi và chỉ khi
khi và chỉ khi ![]()
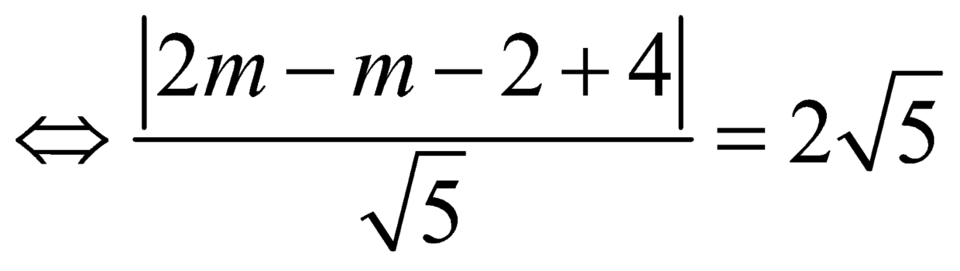
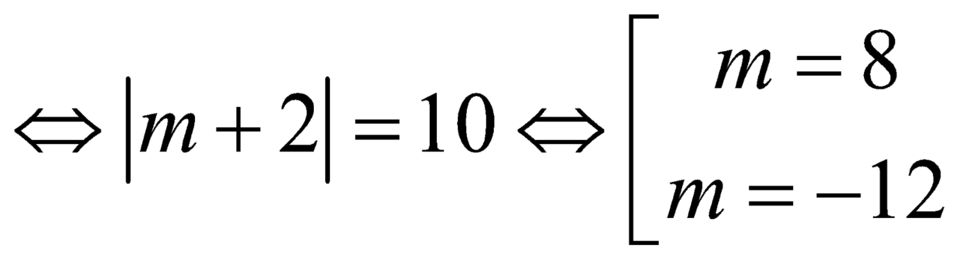 .
.
Vậy ![]() .
.

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.
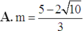
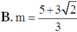
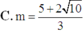
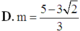
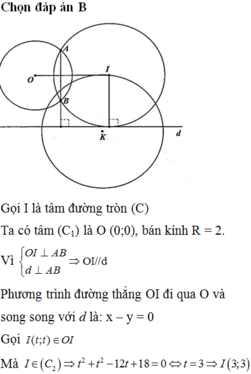

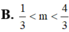
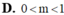
Đáp án C
Xét đường cong (C1): f(x) = 3x(3x - m + 2) + m2 - 3m
Và đường cong (C2): g(x) = 3x + 1
Để (C1) tiếp xúc với (C2) ⇔ f ' ( x ) = g ' ( x ) f ( x ) = g ( x )