
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)

Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên

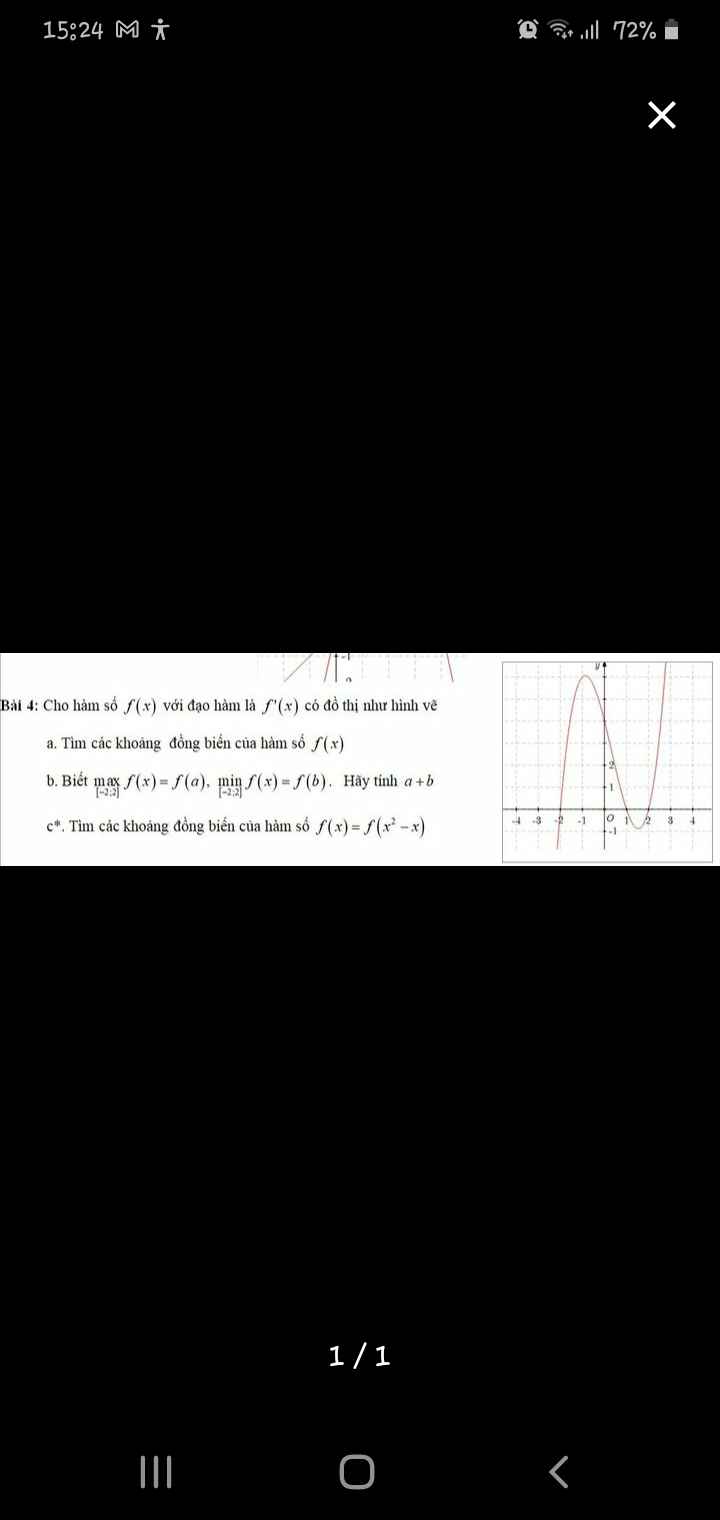
Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:
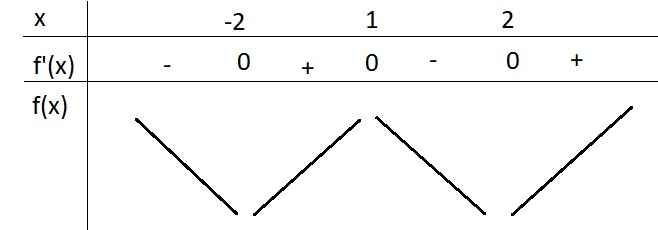
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)
Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)
Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)
\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)
\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(2\right)>f\left(-2\right)\)
\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)
\(\Rightarrow a+b=1+\left(-2\right)=-1\)

Từ đồ thị ta thấy \(f'\left(x\right)>0\) trên các khoảng \(\left(-1;1\right)\) và \(\left(3;+\infty\right)\)
\(f'\left(x\right)< 0\) trên \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
\(\Rightarrow\) Hàm nghịch biến trên (1;3)

Chỉ thấy bài 5 với 6:
5.
\(f'\left(x\right)+2f\left(x\right)=0\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int-2dx\Rightarrow ln\left(f\left(x\right)\right)=-2x+C\)
Thay \(x=1\Rightarrow0=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left(f\left(x\right)\right)=-2x+2\Rightarrow f\left(x\right)=e^{-2x+2}\)
\(\Rightarrow f\left(-1\right)=e^4\)
6.
\(f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow x'.f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow\left[x.f\left(x\right)\right]'=2x+1\)
Lấy nguyên hàm 2 vế:
\(\int\left[x.f\left(x\right)\right]'dx=\int\left(2x+1\right)dx\)
\(\Rightarrow x.f\left(x\right)=x^2+x+C\)
Thay \(x=1\Rightarrow1.f\left(1\right)=1+1+C\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2+x+1}{x}\)
\(\Rightarrow f\left(2\right)=\dfrac{7}{2}\)

Hôm bữa bên CLB của ĐH Bách Khoa Hồ Chí Minh có tổ chức ấy bạn, cơ mà chắc hết rùi :D Btw, có thầy gì admin page Luyện thi đánh giá năng lực hồi năm ngoái mình có follow thấy thầy cũng tổ chức thường xuyên lắm nè :v

a) \(I_1=\int\dfrac{dx}{x^2+2x+3}\)
\(=\int\dfrac{dx}{\left(x+1\right)^2+2}=\int\dfrac{d\left(x+1\right)}{\left(x+1\right)^2+\left(\sqrt{2}\right)^2}\)
\(=\dfrac{1}{\sqrt{2}}arctan\left(\dfrac{x+1}{\sqrt{2}}\right)+C\)
b) \(I_2=\int\dfrac{dx}{4x^2+4x+2}\)
\(=\int\dfrac{dx}{\left(2x+1\right)^2+1}=\dfrac{1}{2}\int\dfrac{d\left(2x+1\right)}{\left(2x+1\right)^2+1^2}\)
\(=\dfrac{1}{2}arctan\left(2x+1\right)+C\)

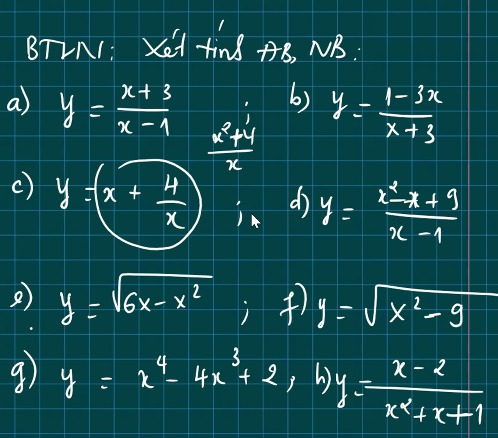 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ

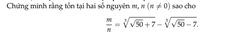



Lời giải:
a. Sau 2 năm thu được:
$100(1+\frac{0,5}{100})^{24}=112,72$ (triệu đồng)
b.
Giả sử sau $n$ tháng thì rút ra được gốc lẫn lãi là 300 triệu
$100(1+0,005)^n=300$
$1,005^n=3$
$n=\log_{1,005}3=220,3$ (tháng)
Vậy sau ít nhất 221 tháng thì người đó rút được 300 triệu. Đổi 221 tháng thành 18 năm 5 tháng
Đáp án C.
Em cảm ơn cô ạ