Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
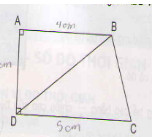
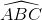là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra
= 
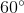và =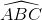 
.
= 
- 
= - = 
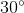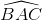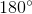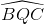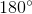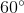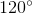(tổng các góc của một tứ giác bằng 
)
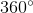a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.
a)Gọi I là trung điểm BC \(\Rightarrow\hept{\begin{cases}OI\perp BC\\BI=CI=\frac{R\sqrt{3}}{2}\end{cases}}\)Ta có\(\sin\widehat{BOI}=\frac{BI}{OB}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\Rightarrow\widehat{BOI}=60^o\) \(\Rightarrow\widehat{BOC}=120^o\)
b) Ta có \(\widebat{BC}=\widehat{BOC}=120^o\) Mà\(\Rightarrow\widehat{BAC}=\frac{\widebat{BC}}{2}\)\(\Rightarrow\widehat{BAC}=60^o\)