Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Ta co \(AC^2+BD^2=MA^2+MC^2+MB^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)=AD^2+BC^2\)
Kẻ đường kính CE ta có \(\widehat{CDE}=90^0\)
Hay \(CD\perp DE\)
\(\Rightarrow DE\)// \(AB\) nên tứ giác ABED là hình thang cân
\(\Rightarrow AD=BE\)
Ta có : \(AD^2+BC^2=BE^2+BC^2=CE^2=4R^2\) không dổi
b ) Vì IB = IC = IM nên \(IO^2+IM^2=OC^2-IM^2+IM^2=R^2\)
Gọi J là trung điểm của MO . Áp dụng công thức đường trung tuyến trong \(\Delta IMO\) Ta có : \(IJ=\sqrt{\frac{IO^2+IM^2}{2}-\frac{MO^2}{4}}=\sqrt{\frac{R^2}{2}-\frac{MO^2}{4}}\) ( không dổi vì OM cố định ) Do đó I chạy trên đường tròn tâm J bán kính IJ không đổi Chúc bạn học tốt !!
O A C B D I M N E F P H
a) Kẻ đường kính DP của (O), ta có: BD vuông góc BP. Mà BD vuông góc AC nên BP // AC
=> (AP = (BC => (AB = (CP => AB = CP => AB2 + CD2 = CP2 + CD2 = DP2 = 4R2 (ĐL Pytagore)
Tương tự: AD2 + BC2 = 4R2 => ĐPCM.
b) Ta có: AB2 + BC2 + CD2 + DA2 = 4R2 + 4R2 = 8R2
Ta lại có: AC2 + BD2 = IA2 + IB2 + IC2 + ID2 + 2.IB.ID + 2.IA.IC = AB2 + CD2 + 4.IE.IF
= 4R2 + 4(R+d)(R-d) = 4R2 + 4R2 - 4d2 = 8R2 - 4d2
c) Gọi tia NI cắt AB tại H. Dễ thấy: ^BIH = ^NID = ^NDI = ^IAB = 900 - ^IBA => IN vuông góc AB.
C/m tương tự, ta có: IM vuông góc CD => ĐPCM.
d) Đường tròn (O): Dây AB, M trung điểm AB => OM vuông góc AB. Mà AB vuông góc IN => OM // IN
Tương tự ON // IM. Do đó: Tứ giác OMIN là hình bình hành (đpcm).
e) Vì tứ giác OMIN là hình bình hành nên MN đi qua trung điểm OI. Mà OI cố định NÊN trung điểm của OI cũng cố định nên ta có đpcm.
Chậc -_- bài này mình làm được lâu rồi bạn à :V Nhưng cũng cảm ơn , tớ nhờ cậu bài khác mà :(

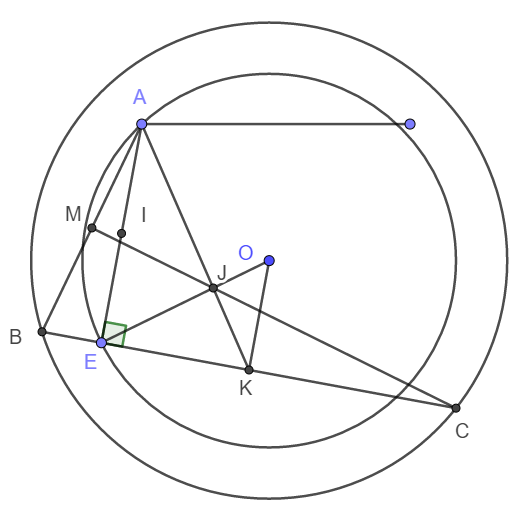
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

Bài 1 :
Áp dụng Cô - si ta có :
\(\frac{a+1}{b^2+1}=\left(a+1\right)-\frac{\left(a+1\right)b^2}{b^2+1}\le\left(a+1\right)-\frac{\left(a+1\right)b^2}{2b}\)\(=\left(a+1\right)-\frac{ab+b}{2}\)
Tương tự ta cũng có : \(\frac{b+1}{c^2+1}\le\left(b+1\right)-\frac{bc+c}{2};\frac{c+1}{a^2+1}\le\left(c+1\right)-\frac{ca+a}{2}\)
Cộng vế theo vế ta được:
\(\frac{a+1}{b^2+1}+\frac{b+1}{c^2+1}+\frac{c+1}{a^2+1}\)\(\ge a+b+c+3-\frac{ab+bc+ca+a+b+c}{2}\)
\(\ge6-\frac{ab+bc+ca+3}{2}\)
Mặt khác ta có BĐT : \(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\Leftrightarrow ab+bc+ca\le3\)
Do đó : \(\frac{a+1}{b^2+1}+\frac{b+1}{c^2+1}+\frac{c+1}{a^2+1}\ge3\)
Dấu " = " xảy ra khi và chỉ khi \(a=b=c=1\)
Bài 2 :
A B C D M N P Q O K I H
a) Ta có : \(MI=MA,QI=QD\)nên \(MQ\)là đường trung bình \(\Delta AID\)
\(\Rightarrow MQ//AD\)
Tương tự NP là đường trung bình của \(\Delta BIC\)
\(\Rightarrow NP//BC\)
Do đó : \(NMQ=BAD=NPQ\)nên tứ giác MPNQ nội tiếp
b ) Kẻ \(OH\perp AB\)tại H và \(OK\perp CD\)tại K
Ta có : \(AB\perp CD\)
\(\Rightarrow OHIK\)là hình chữ nhật
Do đó \(AB^2+CD^2=4\left(BH^2+CK^2\right)=4\left(R^2-OH^2+R^2-OK^2\right)\)
\(=4\left(2R^2-OI^2\right)\)
Diện tích tứ giác MPNQ là : \(\frac{MN.PQ}{2}=\frac{AB.CD}{8}\le\frac{\left(AB+CD\right)^2}{16}=\frac{2R^2-OI^2}{4}\)không đổi
GTLN của diện tích tứ giác MNPQ là : \(\frac{2R^2-OI^2}{4}\), khi đó \(AB=CD\)
Chúc bạn học tốt !!!

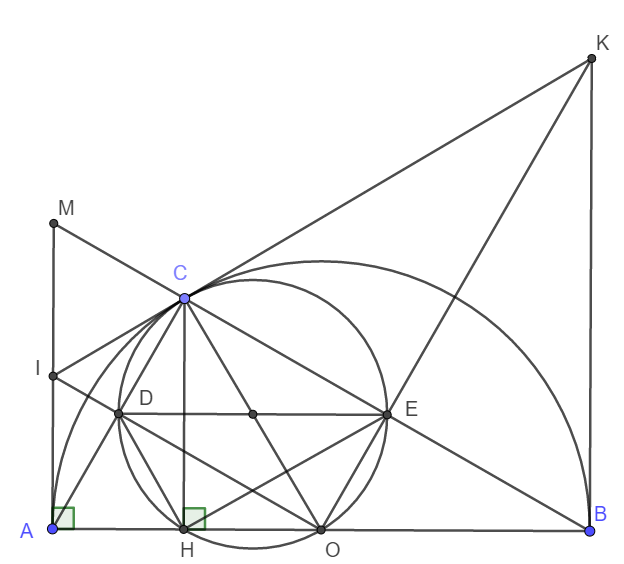
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.
A B C D E M J O I
a) Ta có :
\(AC^2+BD^2=MA^2+MC^2+MB^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)=AD^2+BC^2\)
Kẻ đường kính CE ta có \(\widehat{CDE}=90^0\) hay \(CD\perp DE\)
\(\Rightarrow DE//AB\)nên tứ giác ABED là hình thang cân
\(\Rightarrow AD=BE\)
Ta có : \(AD^2+BC^2=BE^2+BC^2=CE^2=4R^2\)không đổi
b ) \(IB=IC=IM\)nên \(IO^2+IM^2=OC^2-IM^2+IM^2=R^2\)
Gọi J là trung điểm của MO . Áp dụng công thức đường trung tuyến trong \(\Delta IMO\)
Ta có : \(IJ=\sqrt{\frac{IO^2+IM^2}{2}-\frac{MO^2}{4}}=\sqrt{\frac{R^2}{2}-\frac{MO^2}{4}}\)( không đổi vì O,M cố định )
Do đó I chạy trên đường tròn tâm J bán kính IJ không đổi.
Chúc bạn học tốt !!!