Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do \(OA=OB\) (2 bán kính)
=> Tam giác OAB cân tại O
Mà OH là đường trung tuyến
=> OH cũng là đường cao ứng với AB
=> OH vuông góc AB.
(VẬY TA CÓ ĐPCM).
b) Có: góc CDA là góc nội tiếp chắn nửa đường tròn
=> góc CDA = 90 độ
=> CD vuông góc AD
Xét tam giác CAK vuông tại A (gt) và AD vuông góc CK (CMT)
=> Áp dụng HTL thì: \(CD.CK=CA^2=2\left(OA\right)^2=4R^2\)
VẬY TA CÓ ĐPCM.
c) Có: \(sinC=\frac{AD}{AC};cosC=\frac{CD}{AC}\)
=> \(2R.sinC.cosC=2R.\left(\frac{AD.CD}{AC^2}\right)=2R.\left(\frac{AD.CD}{CD.CK}\right)=2R.\left(\frac{AD}{CK}\right)\) (HTL: \(AC^2=CD.CK\))
=> \(\frac{AD^2}{2R.sinC.cosC}=\frac{AD^2}{\frac{2R.AD}{CK}}=\frac{AD^2.CK}{2R.AD}=\frac{AD.CK}{2R}=\frac{AD.CK}{AC}\)
Áp dụng tiếp tục HTL ta được:
=> \(AD.CK=AC.AK\)
=> \(VP=\frac{AC.AK}{AC}=AK\)
VẬY TA CÓ ĐPCM.
Câu d nhaaaaaaaaa !!!!!
Có: OA; OB là 2 tiếp tuyến của O và cắt nhau tại K
=> Áp dụng tính chất 2 tiếp tuyến cắt nhau ta được:
=> OK vuông góc với AB.
Tương tự thì: OC và OD cũng là 2 tiếp tuyến của O và cắt nhau tại E
=> Áp dụng tính chất 2 tiếp tuyến cắt nhau ta được:
=> OE vuông góc với CD.
* Áp dụng HTL vào tam giác OAK vuông tại A có AH vuông góc với OK:
=> \(OH.OK=OA^2\)
* Áp dụng HTL vào tam giác OCE vuông tại C có CI vuông góc với OE:
=> \(OI.OE=OC^2\)
Mà: \(OA=OE\) {2 BÁN KÍNH CỦA (O)}
=> \(OH.OK=OI.OE\)
(VẬY TA CÓ ĐPCM).

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CA⊥CB
mà CA⊥OH
nên OH//BC
b: Xét (O) có
OH là một phần đường kính
AC là dây
OH⊥AC tại H
Do đó: H là trung điểm của AC
Xét ΔMAC có
MH là đường trung tuyến
MH là đường cao
Do đó: ΔMAC cân tại M
Xét ΔOAM và ΔOCM có
OA=OC
MA=MC
OM chung
Do đó:ΔOAM=ΔOCM
Suy ra: \(\widehat{OAM}=\widehat{OCM}=90^0\)
hay MA là tiếp tuyến của (O)

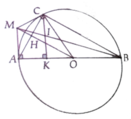
a, HS tự làm
b, HS tự làm
c, IK = 1 2 CK = 1 2 AC.sinα = R.cosα.sinα
d, Giả sử BI cắt AM tại N. Vì IK//AM => MO = OP
=> 1 O I 2 = 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => M ≡ N