Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

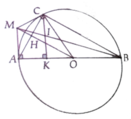
a, HS tự làm
b, HS tự làm
c, IK = 1 2 CK = 1 2 AC.sinα = R.cosα.sinα
d, Giả sử BI cắt AM tại N. Vì IK//AM => MO = OP
=> 1 O I 2 = 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => M ≡ N

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CA⊥CB
mà CA⊥OH
nên OH//BC
b: Xét (O) có
OH là một phần đường kính
AC là dây
OH⊥AC tại H
Do đó: H là trung điểm của AC
Xét ΔMAC có
MH là đường trung tuyến
MH là đường cao
Do đó: ΔMAC cân tại M
Xét ΔOAM và ΔOCM có
OA=OC
MA=MC
OM chung
Do đó:ΔOAM=ΔOCM
Suy ra: \(\widehat{OAM}=\widehat{OCM}=90^0\)
hay MA là tiếp tuyến của (O)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Ta có: ΔOAC cân tại O(OA=OC)
mà OH là đường trung tuyến
nên OH\(\perp\)AC và OH là tia phân giác của góc AOC
Ta có: OH\(\perp\)AC(cmt)
AC\(\perp\)CB tại C(Do ΔACB vuông tại C)
Do đó: OH//BC
b:
OH là phân giác của góc AOC
=>\(\widehat{AOH}=\widehat{COH}\)
mà M\(\in\)OH
nên \(\widehat{AOM}=\widehat{COM}\)
Xét ΔOCM và ΔOAM có
OC=OA
\(\widehat{COM}=\widehat{AOM}\)
OM chung
Do đó: ΔOCM=ΔOAM
=>\(\widehat{OCM}=\widehat{OAM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{OAM}=90^0\)
=>OA\(\perp\)MA tại A
=>MA là tiếp tuyến tại A của (O)
