Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

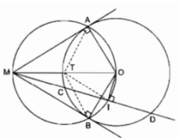
Khi cát tuyến MCD không đi qua O.
IC = ID (gt)
OI ⊥ CD (đường kính đi qua điểm chính giữa của dây không đi qua tâm)

A, I, B nhìn MO dưới một góc bằng 90º nên A, I, B nằm trên đường tròn đường kính MO.
Vậy: Ngũ giác MAOIB nội tiếp.
(Khi cát tuyến MCD đi qua O ngũ giác MAOIB suy biến thành tứ giác MAOB chứng minh tương tự).

a: ΔOCD cân tại O
mà OI là trung tuyến
nên OI là đường cao
Xét tứ giác MAOI có
góc MAO=góc MIO=90 độ
nên MAOI là tứ giác nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MC*MD

a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b; Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB

a) Ta có CA,CM là các tiếp tuyến từ C tới đường tròn (O) => OC là phân giác của ^AOM => ^MOC = ^AOC
Ta thấy ^CMD là góc chắn nửa đường tròn (I) => ^CMD = 900 => ^CMD + ^CMO = 1800
=> 3 điểm D,M,O thẳng hàng => ^DOC = ^MOC. Mà ^MOC = ^AOC nên ^DOC = ^AOC
Hai đường tròn (O),(I) cùng tiếp xúc với a => CD // AB (Cùng vuông góc với a)
Do đó ^AOC = ^DCO (So le trong) => ^DOC = ^DCO => \(\Delta\)ODC cân tại D
Lại có DK vuông góc OC tại K (Vì ^DKC chắn nửa đường tròn) => K là trung điểm OC (đpcm).
b) Gọi đường thẳng qua D vuông góc với BC cắt BC,AB lần lượt tại H,S.
Dễ thấy điểm H nằm trên đường tròn (I) => ^HMO = ^HCD = ^HBO (Do CD // AB)
=> Tứ giác HOBM nội tiếp => ^OHB = ^OMB => 900 - ^OHB = 900 - ^OMB
=> ^OHS = 900 - ^ABM = ^MAB = ^ACO (Cùng phụ ^CAM) (1)
Ta lại có ^SHK = ^DCK = ^SOK (Vì AB // CD) => Tứ giác KHOS nội tiếp => ^OHS = ^OKS (2)
Từ (1) và (2) suy ra ^ACO = ^OKS => KS // AC. Xét \(\Delta\)CAO có:
K là trung điểm cạnh OC (cmt), KS // AC (cmt), S thuộc OA => S là trung điểm cạnh OA
Do 2 điểm O,A cố định nên S cũng cố định. Mà đường thẳng qua D vuông góc BC cắt OA tại S
Nên ta có ĐPCM.

a: ΔOCD cân tại O
mà OH là đường trung tuyến
nên OH vuông góc CD
=>OH vuông góc với HM
=>H nằm trên đường tròn đường kính OM
b: \(CH=HD=\dfrac{CD}{2}=\dfrac{R\sqrt{3}}{2}\)
ΔOHD vuông tại H
=>OH^2+HD^2=OD^2
=>\(OH^2+R^2\cdot\dfrac{3}{4}=R^2\)
=>\(OH^2=\dfrac{1}{4}R^2\)
=>OH=R/2
Xét ΔCOD có \(cosCOD=\dfrac{OC^2+OD^2-CD^2}{2\cdot OC\cdot OD}=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)
=>góc COD=120 độ

CD và AB là gì vậy bạn
nói rõ đi
Phải có là dây CD khác dây AB chứ bạn:
M là TĐ AB thì OM vuông góc với AB,ta giả sử M là trung điểm CD thì OM vuông góc với CD
>>>CD cắt AB hoặc CD//AB.
Mà CD cắt AB và CD không trùng với AB,suy ra OMC và OMC khác OMA=90 độ,
>>>M không là trung điểm CD(đpcm)