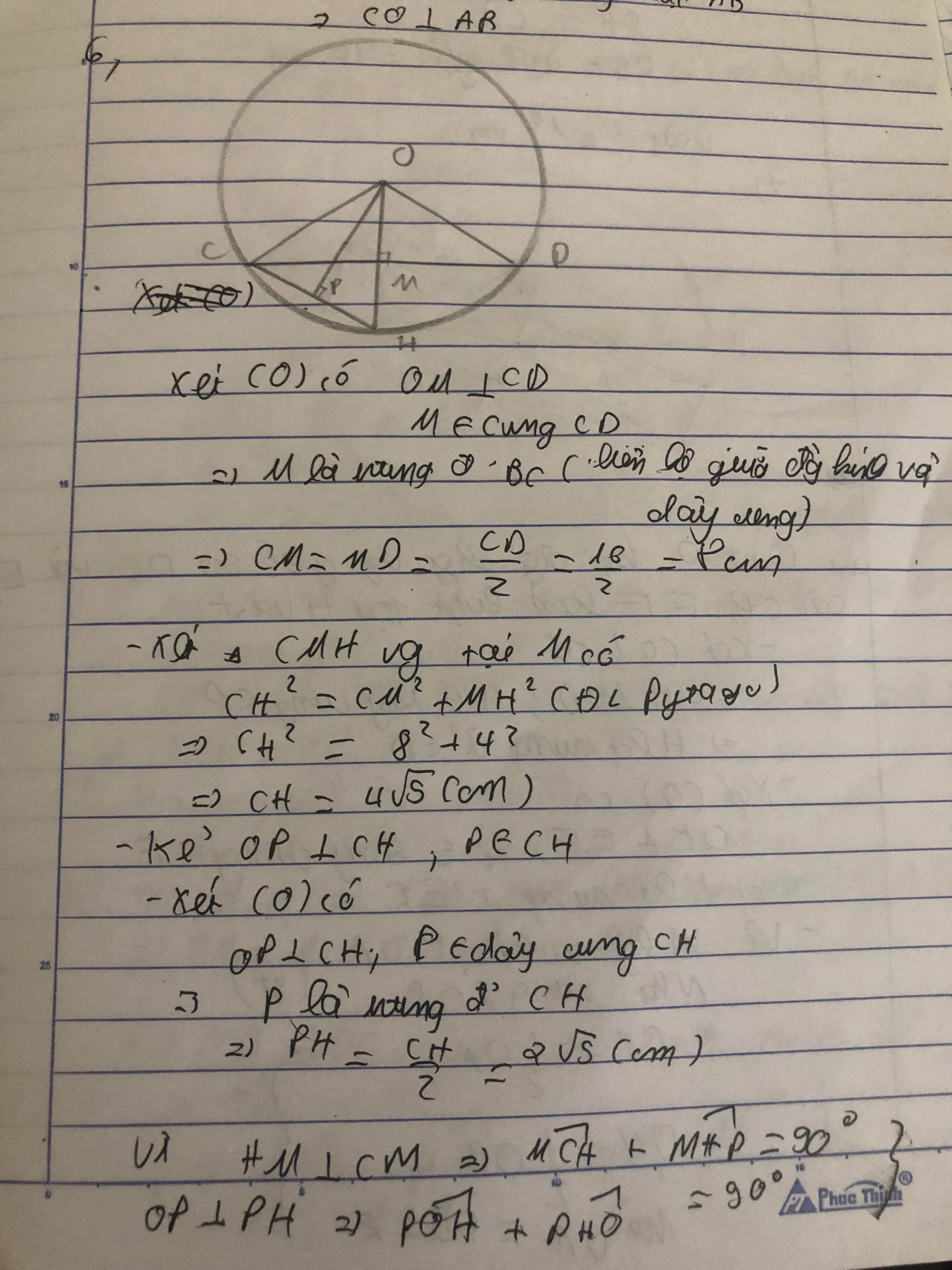
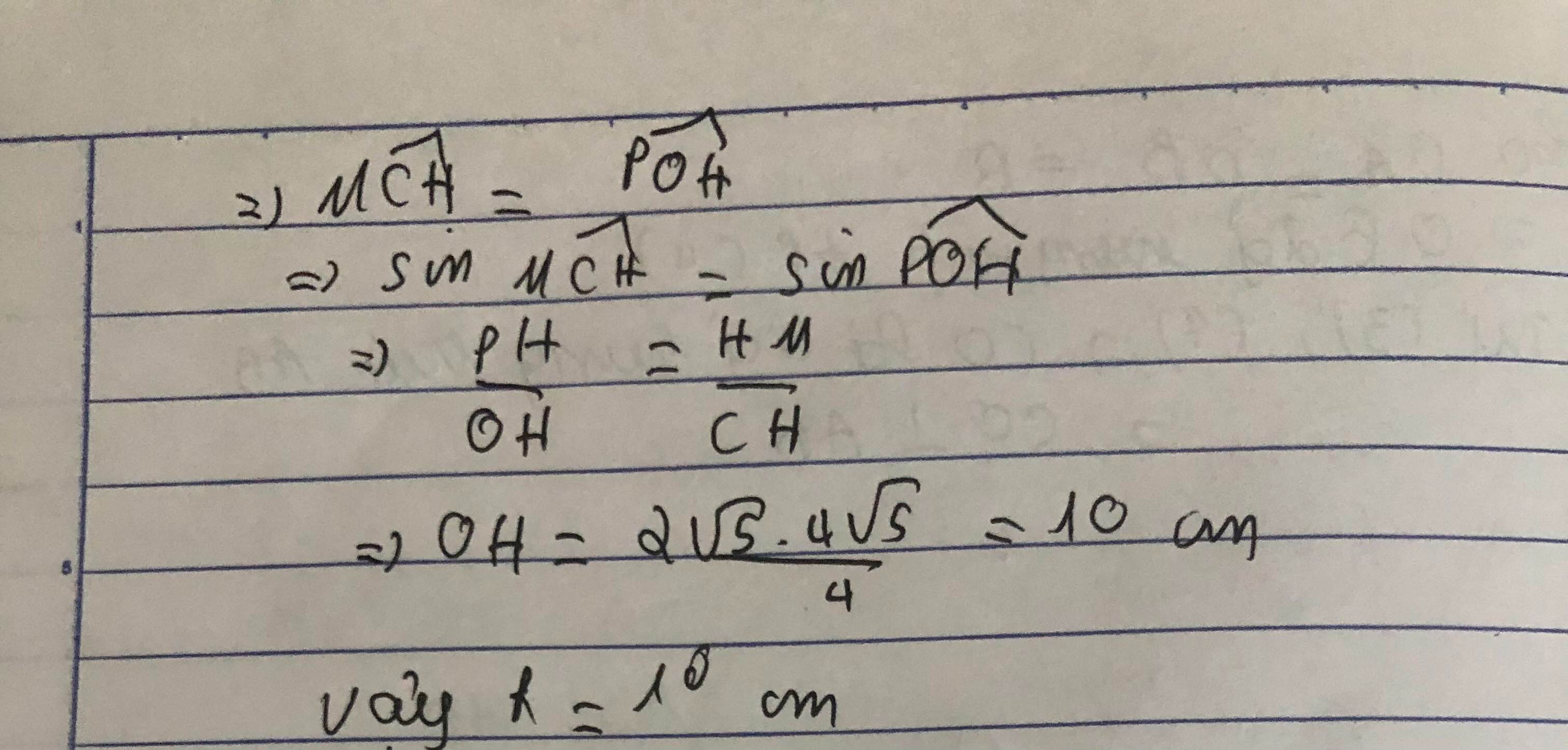
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
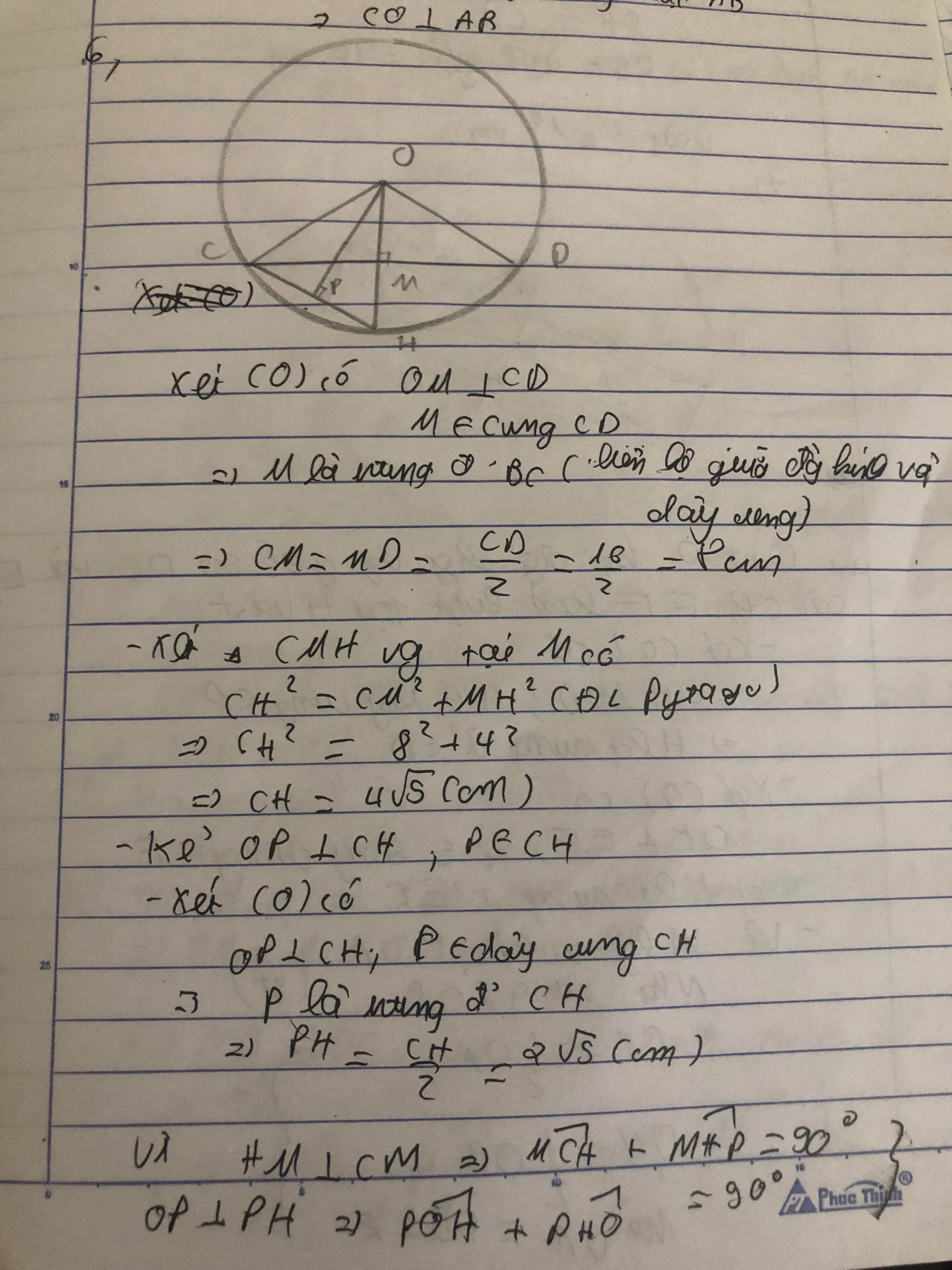
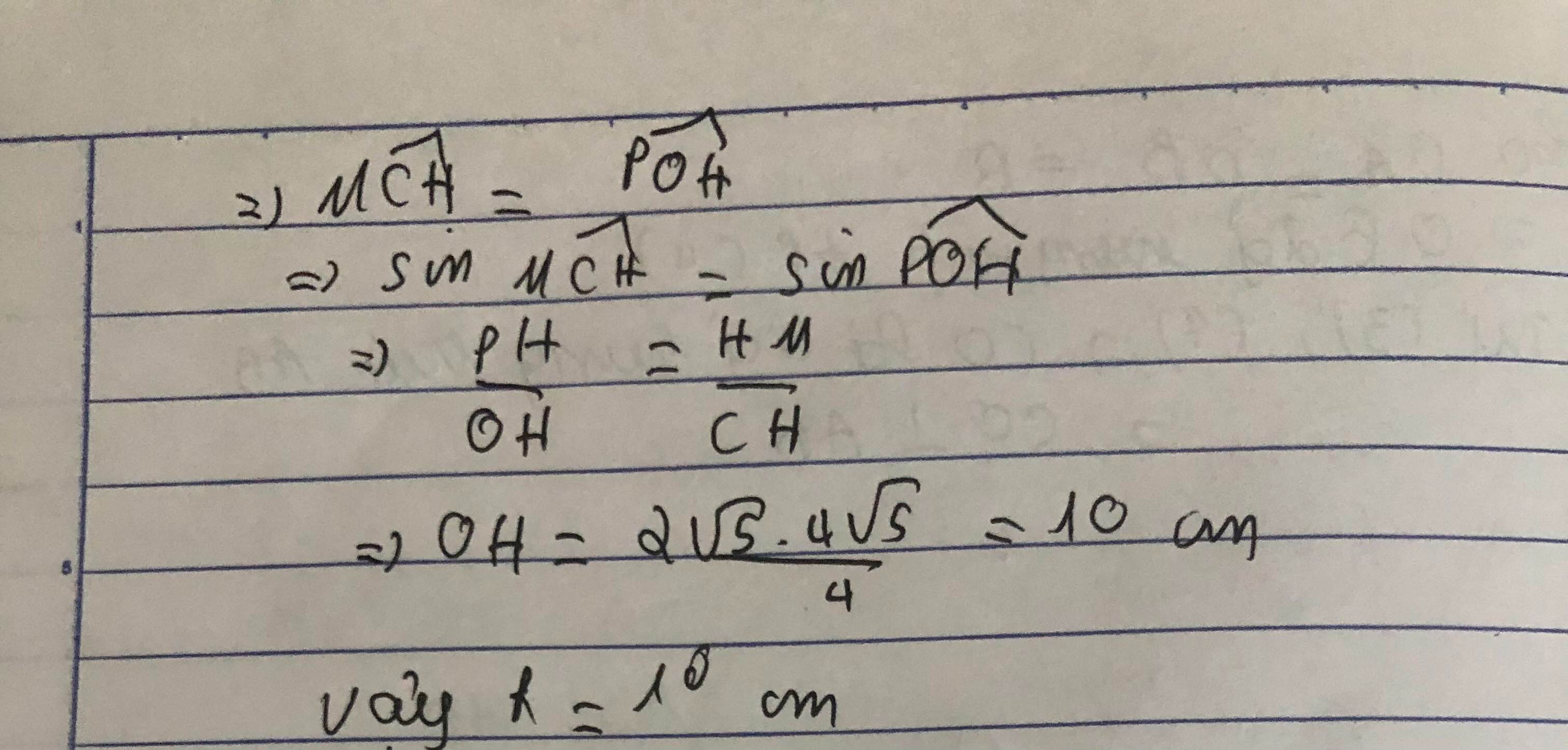
Đặt OH = x cm (R = OH)
Ta có OM = x – 4 cm
Áp đụng định lý Pytago ta tìm được x = 10cm
Kéo dài HO về phía O cắt (o) tại K => KH là đường kính (o). Nối CH; CK ta có
^KCH=90 (góc nội tiếp chắn nửa đường tròn)
CM=DM=CD/2=8 cm (bán kính vuông góc với dây cung thì chia đôi dây cung)
Xét tg vuông KCH có \(CM^2=MH.MK\Rightarrow8^2=4.MK\Rightarrow MK=16cm\)
\(\Rightarrow KH=MH+MK=4+16=20cm\Rightarrow OK=\frac{KH}{2}=10cm\)
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
Lời giải:
Vì tam giác $OCD$ cân tại $O$ nên đường cao $OM$ đồng thời cũng là đường trung tuyến
\(\Rightarrow CM=DM=\frac{CD}{2}=8\)
Đặt \(MO=a\Rightarrow OH=MH+MO=4+a\)
Áp dụng định lý Pitago:
\(CM^2+MO^2=CO^2=R^2=OH^2\)
\(\Leftrightarrow 8^2+a^2=(a+4)^2\)
\(\Leftrightarrow 8a=48\Rightarrow a=6\)
Do đó bán kính của $(O)$ là: \(R=OH=a+4=6+4=10\) (cm)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
ΔAOI vuông tại O
=>AO^2+OI^2=AI^2
=>AI^2=4^2+3^2=25
=>AI=5cm
Xét ΔAOI vuông tại O và ΔAMB vuông tại M có
góc OAI chung
Do đó: ΔAOI đồng dạng với ΔAMB
=>AO/AM=AI/AB
=>4/AM=5/8
=>AM=4*8/5=6,4cm
ΔAMB vuông tại M
=>AM^2=AB^2+MB^2
=>MB^2=8^2-6,4^2=4,8^2
=>MB=4,8cm
ΔMAB vuông tại M có MH là đường cao
nên MH*AB=MB*MA
=>MH*8=4,8*6,4
=>MH=3,84(cm)
