Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc AKB=1/2*180=90 độ
góc HCB+góc HKB=180 độ
=>BKHC nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chug
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AC*AB=1/2R*2R=R^2
Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)
Mà AK giao MN tại H =) Góc HKP = 90độ (1)
Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)
Từ (1) và (2) =) góc HKP + góc HCP = 180độ
Mà 2 góc đối nhau
=) Tứ giác BCHK nội tiếp
1) Xét (O) có
ΔKAB nội tiếp đường tròn(K,A,B\(\in\)(O))
AB là đường kính
Do đó: ΔKAB vuông tại K(Định lí)
\(\Leftrightarrow\widehat{AKB}=90^0\)
hay \(\widehat{HKB}=90^0\)
Xét tứ giác BKHC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BKHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,K,H,C cùng thuộc một đường tròn(đpcm)
a.
Góc AKB là góc nội tiếp chắn nửa (O) nên ∠AKB=90o∠AKB=90o
Khi này dễ dàng có đpcm
b.
Do C là trung điểm OA nên AC=OA2=R2AC=OA2=R2
Tứ giác BCHK nội tiếp nên chứng minh được △AHC∼△ABK△AHC∼△ABK
Từ đó: ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2
c.
Lấy điểm E trên tia đối của BK sao cho KE=KM=KI
Chứng minh được tam giác AMO đều (có 3 cạnh = nhau) khi đó ∠MAB=60o∠MAB=60o
Dễ dàng chứng minh được tứ giác ABKM nội tiếp nên ∠MKE=∠MAB=60o∠MKE=∠MAB=60o
khi đó tam giác MKE đều nên ME = MK(1)
Có ∠CMB=∠MAB=6oo∠CMB=∠MAB=6oo (hai góc cùng phụ với góc AMC) nên
∠MNK=∠BME(2)∠MNK=∠BME(2)
Góc CMB=60oCMB=60o nên MB=2MCMB=2MC mà MN=2MCMN=2MC nên MN=MB(3)MN=MB(3)
Từ (1),(2) và (3) nên △NMK=△BME△NMK=△BME nên NK=BENK=BE hay NI+IK=BK+KINI+IK=BK+KI từ đó có đpcm
Hình gửi kèm
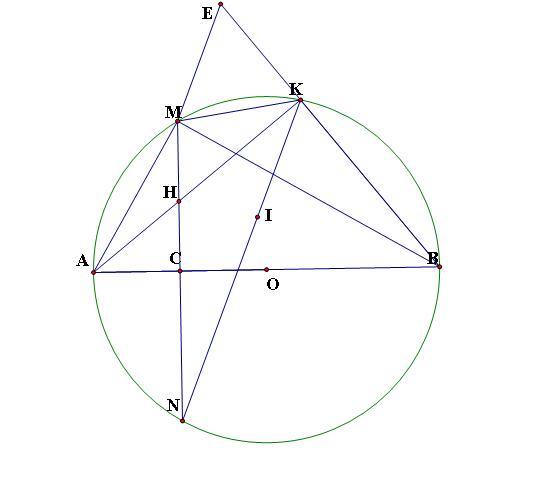
Mình giải giúp câu a, b, cho bạn nhé bạn
a, tam giác ABK có : AB là đường kính ; K thuộc (O)
suy ra góc AKB = 90 độ
Xét tứ giác BCHK có : góc MCB + góc AKB = 90 độ + 90 độ = 180 độ
suy ra tứ giác BCHK nội tiếp đường tròn
b, xét tam giác ACH và tam giác AKB có ;
góc A chung
góc ACH = góc AKB = 90 độ
suy ra tam giác ACH đồng dạng với tam giác AKB (g. g)
suy ra AH/AB = AC/AK hay AH/2R = R chia 2/AK
khi và chỉ khi AH . AK = 2R . R/2 = R bình
vậy AH.AK= R bình