Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(C): x^2+y^2-4x+6y-12=0
=>O(2;-3)
R=căn 2^2+(-3)^2+12=5
Gọi đường cần tìm là (d'): x+y+c=0
Gọi A,B lần lượt là giao điểm của (d') và (C)
ΔOHB vuông tại H
\(d\left(O;AB\right)=\dfrac{\left|2+\left(-3\right)+c\right|}{\sqrt{2}}=HO\)
\(=\sqrt{OB^2-BH^2}=3\)
=>\(\left[{}\begin{matrix}c=3\sqrt{2}+1\\c=-3\sqrt{2}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x+y-3\sqrt{2}+1=0\\x+y+3\sqrt{2}+1=0\end{matrix}\right.\)

Đường tròn (C): x 2 + y 2 − 6 x + 8 y − 24 = 0 có tâm I(3; - 4) và bán kính R = 7.
Khoảng cách d I , ∆ = 4.3 + 3. − 4 − m 5 = m 5 .
Để đường thẳng cắt đường tròn theo dây cung có độ dài bằng 10 ta có:
10 = 2 R 2 − d ( I ; Δ ) 2 ⇔ 5 = 49 − m 2 25 ⇔ 25 = 49 − m 2 25 ⇔ m 2 25 = 24 ⇔ m 2 = 600 ⇔ m = ± 10 6
ĐÁP ÁN B

Đáp án C
- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0
- IH là khoảng cách từ I đến d’:
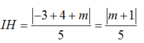
- Xét tam giác vuông IHB:

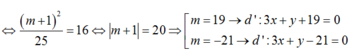

(C) có tâm I(2;-1), bán kính R=\(\sqrt{6}\). Khoảng cách từ tâm I tới $\Delta$ là
$d=\dfrac{|2.2-(-1)|}{\sqrt{2^2+1}}=\sqrt{5}<R$ nên $\Delta$ cắt (C).
Gọi $l$ là độ dài dây cung thì
$$\dfrac{l}{2}=\sqrt{R^2-d^2}=1\Rightarrow l=2$$

(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C