Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Tọa độ A là nghiệm của hệ
\(\hept{\begin{cases}y=-2x+3\\y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1,5\\y=0\end{cases}}\)
=> A(1,5; 0)
Tọa độ B là nghiệm của hệ
\(\hept{\begin{cases}x=0\\y=-2x+3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=3\end{cases}}\)
=> B(0; 3)
Khoản cách từ O(0; 0) đến d
\(=\frac{\left|0-2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{3}{\sqrt{5}}\)
b/ Khoản cách từ C(0; - 2) đến d là
\(d\left(C,d\right)=\frac{\left|-2+2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{5}{\sqrt{5}}=\sqrt{5}\)
A/ TỌA ĐỘ A THỎA \(\hept{\begin{cases}Y=0\\Y=-2X+3\end{cases}}\)\(\Rightarrow\Rightarrow A\left(\frac{3}{2},O\right)\)
TỌA ĐỘ B THỎA,\(\hept{\begin{cases}Y=-2X+3\\X=0\end{cases}}\)\(\Rightarrow B\left(0,3\right)\)
GOI H LA HINH CHIEU CUA O LEN (d) ap dung he thuc luong trong tam giac vuongOAB cho
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\Leftrightarrow\frac{1}{OH^2}=\frac{1}{\left(\frac{3}{2}\right)^2}+\frac{1}{3^2}\Rightarrow AH=\frac{3}{\sqrt{5}}\)
B/GỌI K LÀ HÌNH CHIẾU CỦA C LÊN (d) ta co\(\frac{OH}{CK}=\frac{OB}{OC}=\frac{3}{5}\Rightarrow CK=\frac{5}{3}OH=\sqrt{5}\)
(....20 NHA)

Gợi ý :
a) y = 2 => x = 2 hoặc -2 ( do có thể < 0 hay > 0 )
b) S(OAB) = 1 => |x| = 1 => x = 1 hoặc -1
c) Gọi khoảng cách từ O tới (d) là OH
OH bé hơn hoặc bằng khoảng cách 2 của O tới điểm cố định trên Oy
=> max = 2 khi d song^2 Ox => x = 0 => đúng mọi m
d) Thay vào biểu thức hệ thức lượng => khoảng cách từ O tới điểm mà d cắt trên Ox là 0 => d trùng Oy
e) thay x vào có kết quả
f) cắt tại điểm > 2 => biểu thức biểu diễn x > 2 ( -2/(m+3) )

1) \(\left\{{}\begin{matrix}\left(d_1\right):y=2x\\\left(d_2\right):y=-\dfrac{1}{2}x+5\end{matrix}\right.\)
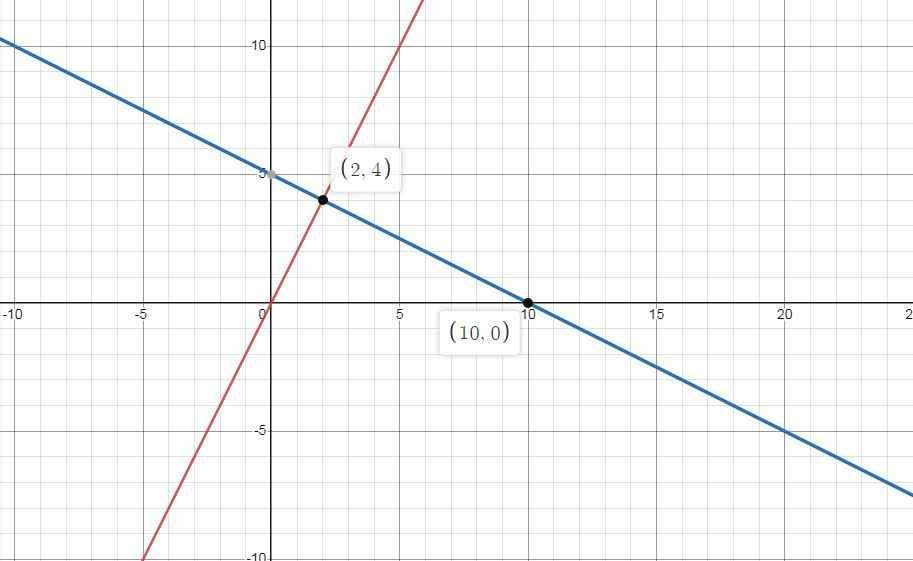
2) Theo đồ thi ta có :
\(\left(d_1\right)\cap\left(d_2\right)=A\left(2;4\right)\)
3) \(\left(d_2\right)\cap Ox=B\left(a;0\right)\)
\(\Leftrightarrow-\dfrac{1}{2}a+5=0\)
\(\Leftrightarrow\dfrac{1}{2}a=5\)
\(\Leftrightarrow a=10\)
\(\Rightarrow\left(d_2\right)\cap Ox=B\left(10;0\right)\)
4) \(OA=\sqrt[]{\left(2-0\right)^2+\left(4-0\right)^2}=\sqrt[]{20}=2\sqrt[]{5}\)
\(OB=\sqrt[]{\left(10-0\right)^2+\left(0-0\right)^2}=\sqrt[]{10^2}=10\)
\(AB=\sqrt[]{\left(10-2\right)^2+\left(0-4\right)^2}=\sqrt[]{80}=4\sqrt[]{5}\)
Ta thấy :
\(OA^2+AB^2=20+80=OB^2=100\)
\(\Rightarrow\Delta OAB\) vuông tại A
\(\Rightarrow\widehat{OAB}=90^o\)
\(sin\widehat{AOB}=\dfrac{AB}{OB}=\dfrac{4\sqrt[]{5}}{10}=\dfrac{2\sqrt[]{5}}{5}\)
\(\Rightarrow\widehat{AOB}\sim63,43^o\)
\(\Rightarrow\widehat{OBA}=90^o-63,43^o=26,57^o\)
5) Chu vi \(\Delta OAB\) :
\(AB+OA+OB=4\sqrt[]{5}+2\sqrt[]{5}+10=10\sqrt[]{5}+10=10\left(\sqrt[]{5}+1\right)\left(đvmd\right)\)
Diện tích \(\Delta OAB\) :
\(\dfrac{1}{2}AB.OA=\dfrac{1}{2}.4\sqrt[]{5}.2\sqrt[]{5}=20\left(đvdt\right)\)



