Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sr vì spam nhưng bn à Vòng 1 | Học trực tuyến
mong bn tự lm bài = chính khả năng của mk

Giải
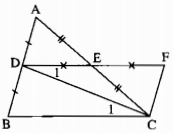
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
ˆAED = CEF^ (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
⇒⇒ AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
⇒ˆADE = CFE^ (2 góc tương ứng)
⇒⇒ AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
ˆBDC = ˆFCD (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: ˆC1 = ˆD1 (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
\(\Delta\)BDC = ∆FCD => BC = DF (hai cạnh tương ứng)
Mà DE = 1 : 2 . DF(gt). Vậy DE = 1 : 2 . BC
a/Xét ΔAED va ΔCEF có:
AE=CE(vì E là trung điểm của AC)
∠AED=∠CEF(đối đỉnh)
ED=EF(vì E là trung điểm của DF)
nên: ΔAED=ΔCEF(c-g-c)
do đó: AD=CF
mà AD=BD (vì D là trung điểm của AB)
vậy BD=CF
b/Ta có: ∠EAD=∠ECF(vì ΔAED=ΔCEF)
mà hai góc này ở vị trí so le trong
nên AB//CF
Ta có:AB//CF(cmt)
nên ∠BDC=∠FCD (hai góc so le trong)
Xét: ΔBDC và ΔFCD có:
DC là cạnh chung
∠BDC=∠FCD(cmt)\
DB=CF(cmt)
nên ΔBDC=ΔFCD(c-g-)
c/Ta có: ∠BCD=∠FDC(vì ΔBDC=ΔFCD)
mà hai góc này ở vị trí so le trong
nên DE//BC
Ta có: \(DE=\dfrac{1}{2}DF\)(vì E là trung điểm của DF)
mà DF=CB(vì ΔFCD=ΔBDC)
vậy \(DE=\dfrac{1}{2}CB\)
A B C F E D

a) Tính số đo góc ABK
Ta có M vừa là trung điểm BC, vừa là trung điểm AK
=> tứ giác ABKC là hình bình hành
=> Góc BAC = góc BKC = 100 độ ; góc ABK = góc KAC
Ta có tổng 4 góc của hình bình hanhg ABKC là 360 độ
=> góc BAC + góc BKC + góc ABK + góc KAC = 360 độ
<=> 200 độ + 2 góc ABK = 360 độ
<=> 2 góc ABK = 160 độ
<=> góc ABK = góc KAC = 60 độ (đpcm)
b) kiểm tra lại đề bài chính xác chưa nhé bạn
a) Tính số đo góc ABK
Ta có M vừa là trung điểm BC, vừa là trung điểm AK
=> tứ giác ABKC là hình bình hành
=> Góc BAC = góc BKC = 100 độ ; góc ABK = góc KAC
Ta có tổng 4 góc của hình bình hanhg ABKC là 360 độ
=> góc BAC + góc BKC + góc ABK + góc KAC = 360 độ
<=> 200 độ + 2 góc ABK = 360 độ
<=> 2 góc ABK = 160 độ
<=> góc ABK = góc KAC = 60 độ (đpcm)

a, Xét △OAC và △OBC
Có: OA = OB (gt)
^AOC = ^BOC (gt)
OC là cạnh chung
=> △OAC = △OBC (c.g.c)
=> ^OAC = ^OBC (2 góc tương ứng) (1)
Ta có: ^OAC + ^CAx = 180o (2 góc kề bù) (2) và ^OBC + ^CBy = 180o (2 góc kề bù) (3)
Từ (1) ; (2) ; (3) => ^CAx = ^CBy
b, Xét △MOA và △MOB
Có: OA = OB (gt)
^MOA = ^MOB (gt)
OM là cạnh chung
=> △MOA = △MOB (c.g.c)
=> MA = MB (2 cạnh tương ứng)
=> M là trung điểm của AB.
c, +) Cách 1: Vì OA = OB (gt) => O thuộc đường trung trực AB
Vì AC = BC (△OAC = △OBC) => C thuộc đường trung trực AB
=> OC là đường trung trực AB
=> OC ⊥ AB => OM ⊥ AB
+) Cách 2: △MOA = △MOB (cmt)
=> ^OMA = ^OMB (2 góc tương ứng)
Mà ^OMA + ^OMB = 180o (2 góc kề bù)
=> ^OMA = ^OMB = 180o : 2 = 90o
=> OM ⊥ AB

A B C M N I a b
a.Tam giác ABC có AB=AC vậy tâm giác ABC là tam giác cân
Vậy xét tam giác AMB và AMC có AB=AC (gt)
góc B=góc C ( tam giác cân)
BM=CM (gt)
Vậy tam giác AMB=tam giác AMC (c.g.c)
b.
Vì tam giác AMB= tam giác AMC nên góc AMC= góc AMB mà AMB + AMC = 180 ( kề bù)
Vậy suy ra AMB=AMC=90 độ vậy AM vuông góc BC
Ta có AM vuông góc BC
AM vuông góc a
Vậy BC//a
c.
Ta có góc NAC=góc ACM( AN//MC)
AC chung
góc NCA= góc MAC ( AM// NC)
Vậy tam giác AMC= tam giác CNA (g.c.g)

Hình bạn tự vẽ nha
Bài làm :
a ) Gọi giao điểm của tia phân giác của góc BAC và đường vuông góc với tia phân giác của BAC là N
Xét tam giác AMD và tam giác AME có :
AMD = AME ( = 90o )
DM : cạnh chung
DAM = EDM ( vì AN là tia phân giác của BAC => BAN = CAN hay DAM = EDM )
DO đó tam giác AMD = tam giác AME ( g . c . g )
=> AD = AE ( hai cạnh tương ứng )
=> tam giác ADE cân tại A ( định nghĩa tam giác cân )
Vì tam giác ADE cân tại A ( cmt )
=> AEM = ADM ( tính chất của tam giác cân ) ( 1 )
Vì BF // AC ( gt ) => BFD = AED ( đồng vị ) ( 2 )
Từ ( 1 ) và ( 2 ) => ADF = BFD hay BDF = BFD
=> tam giác BDF cân tại B ( dấu hiệu nhận biết tam giác cân )
b ) Xét tam giác BFM và tam giác CEM có :
FBM = ECM ( Vì BF // AC ( gt ) )
MB = MC ( vì M là trung điểm của BC ( gt ) )
BMF = CME ( đối đỉnh )
DO đó tam giác BFM = tam giác CEM ( g . c. g )
=> MF = ME ( 2 cạnh tương ứng ) mà MF + ME = EF
=> M là trung điểm của EF
c ) AC - AB = ( AE + EC ) - ( AD - BD )
= AE + EC - AD + BD
= EC + BD ( vì AE = AD ( cmt ) ) ( 1 )
Vì tam giác BDF cân tại B ( CM a ) => BD = BF ( định nghĩa tam giác cân ) ( 2 )
tam giác BFM = tam giác CEM ( CM b ) => BF = EC ( hai cạnh tương ứng ) ( 3 )
Từ 1,2,3 => AC - AB = 2BD
Cảm ơn bạn nguyen duc thang mình cho bạn 3 tk rồi đó