Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M A B H d
H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!

xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)

bạn xem link này nhé mình vừa làm xong :
https://olm.vn/hoi-dap/detail/228037897085.html

Câu hỏi của Nguyễn Thành Nam - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.


a) Giả sử ta kẻ My \(\perp\)BC cắt Bx tại A'
Kết hợp với ^CBx = 450 suy ra \(\Delta\)A'MB vuông cân tại M
=> \(\frac{BM}{BA'}=\frac{1}{\sqrt{2}}\)Lại có \(\frac{BM}{BA}=\frac{1}{\sqrt{2}}\)nên \(BA'\equiv BA\)
\(\Rightarrow A'\equiv A\)nên AM \(\perp\)BC
Kết hợp với CI \(\perp\)AD suy ra N là trực tâm của \(\Delta\)ADC
Suy ra DN \(\perp\)AC (đpcm)
b) Xét \(\Delta\)AMB và \(\Delta\)AMC có:
MB = MC (gt)
^AMB = ^AMC ( = 900)
AM : cạnh chung
Do đó \(\Delta\)AMB = \(\Delta\)AMC (c.g.c)
=> AB = AC (hai cạnh tương ứng) và ^MBA = ^MCA (=450) => ^BAC = 900
Xét \(\Delta\)AIC (^AIC = 900) và \(\Delta\)AHB (^AHB = 900) có:
AB = AC (cmt)
^ABH = ^ACI (cùng phụ với ^BAH)
Do đó \(\Delta\)CIA = \(\Delta\)AHB (ch-gn)
=> AI = BH
=> BH2 + CI2 = AI2 +CI2 =AC2 (không đổi)
c) Xét \(\Delta\)BHM và \(\Delta\)AIM có:
AI = BH (cmt)
^HBM = ^IAM (cùng phụ với hai cặp góc đối đỉnh là ^BDH và ^ADM)
BM = AM (cmt)
Do đó \(\Delta\)BHM = \(\Delta\)AIM
=> HM = IM (1) và ^HMB = ^IMA
Mà ^IMA + ^IMD = 900 nên ^HMB + ^IMD = 900 (2)
Từ (1) và (2) suy ra \(\Delta\)HMI vuông cân tại M => ^HIM = 450
Lại có ^HIC = 900 nên IM là phân giác của ^HIC
Vậy tia phân giác của góc HIC luôn đi qua một điểm cố định M (đpcm)

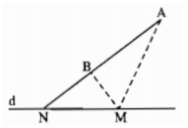
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.
A B d M H
MH \(\perp\)AB
Tam giác AMH vuông tại H ( gt)
Theo định lí Pithagore , ta có : MA2 = AH2 + MH2
Tam giác BMH vuôn tại H (gt)
Theo định lí Pithagore , ta có MB2 = BH2 + MH2
=> AM2 - BM2 = AH2 + MH2 - BH2 - MH2 =AH2 - BH2
Vì AB không đổi ( gt) , d không đổi => AH và BH không đổi
=> AH2 - BH2 không đổi
hay MA2 - MB2 không đổi ( ĐPCM)
#Học-tốt