Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Qua C, kẻ đường thẳng song song với AB cắt AD tại E.
- Xét △ABD có: \(AB\)//\(CE\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{BD}{CD}\) (định lí Ta-let).
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{AB}{AC}\) hay \(CE=AC\).
=>△ACE cân tại C.
=>\(\widehat{EAC}=\widehat{AEC}\).
Mà\(\widehat{AEC}=\widehat{BAD}\) ( \(AB\)//\(CE\) và so le trong).
=>\(\widehat{EAC}=\widehat{BAD}\) hay AD là phân giác của \(\widehat{BAC}\).
Xét tg ABC có
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(gt\right)\)
=>AD là đường phân giác

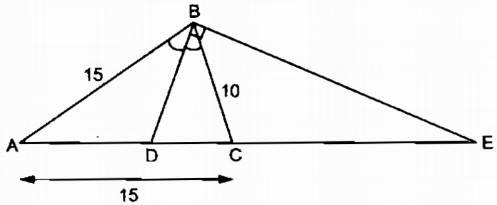
a)
Vì BD là đường phân giác của \(\widehat{ABC}\) nên:
\(\frac{AD}{DC}=\frac{AB}{BC}\)(tính chất đường phân giác )
\(\Rightarrow\frac{AD}{AD+DC}=\frac{AB}{AB+BC}\)hay \(\frac{AD}{AC}=\frac{AB}{AB+BC}\)
Mà \(\Delta\)ABC cân tại A nên AC=AB=15cm
\(\Rightarrow\frac{AD}{15}=\frac{15}{15+10}\Rightarrow AD=\frac{15\cdot15}{25}=9\left(cm\right)\)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)

Xin lỗi mấy bạn . Mình bị thiếu chỗ (cho tam giác ABC vuông tại A)

EZ thôi,vài đường cơ bản;gộp lại cho nó máu ! À mà tính BD chứ nhỉ ??
Kẻ CE là phân giác góc C cắt BD tại E
Đặt EC=x thì BE=x;đặt ED=y
Áp dụng tính chất đường phân giác ta có:
\(\frac{DA}{DC}=\frac{AB}{BC}=\frac{15}{10}=\frac{3}{2}\left(cm\right)\) khi đó \(DA=3a;DC=2a\)
Ta có:\(15=AC=DA+DC=3a+2a=5a\Rightarrow a=3\)
\(\Rightarrow DA=9;DC=6\)
Dễ thấy \(\Delta EDC~\Delta CDB\left(g.g\right)\Rightarrow\frac{ED}{CD}=\frac{DC}{DB}=\frac{EC}{CB}\)
hay \(\frac{y}{6}=\frac{6}{BD}=\frac{x}{10}=\frac{x+y}{10+6}=\frac{x+y}{16}=\frac{BD}{16}\)
\(\Rightarrow BD^2=96\Rightarrow BD=\sqrt{96}\) số khá xấu,ko bt có nhầm lẫn đâu chăng ??

a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=12/8=1,5
=>AD=4,5cm; CD=7,5cm
d: góc ADI=90 độ-góc ABD
góc AID=góc BIH=90 độ-góc DBC
mà góc ABD=góc DBC
nên góc ADI=góc AID
=>ΔAID cân tại A