Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
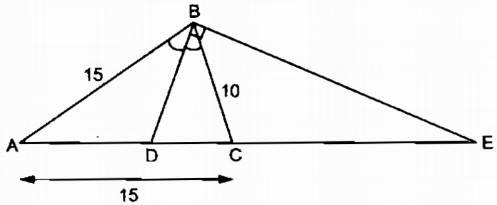
Vì BD là đường phân giác của \(\widehat{ABC}\) nên:
\(\frac{AD}{DC}=\frac{AB}{BC}\)(tính chất đường phân giác )
\(\Rightarrow\frac{AD}{AD+DC}=\frac{AB}{AB+BC}\)hay \(\frac{AD}{AC}=\frac{AB}{AB+BC}\)
Mà \(\Delta\)ABC cân tại A nên AC=AB=15cm
\(\Rightarrow\frac{AD}{15}=\frac{15}{15+10}\Rightarrow AD=\frac{15\cdot15}{25}=9\left(cm\right)\)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)

1)
A B H D c m n
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)

a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm

Bài 1:

Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow\frac{BD}{2}=\frac{DC}{3}=\frac{BD+DC}{2+3}=\frac{BC}{5}\Rightarrow\frac{BD}{BC}=\frac{2}{5}\)
Kẻ \(DK//BE\left(K\in AC\right)\text{ ta có:}\)
\(\frac{AE}{EK}=\frac{AI}{ID}=2;\frac{EK}{EC}=\frac{BD}{BC}=\frac{2}{5}\)
Do đó:\(\frac{AE}{EK}\cdot\frac{EK}{EC}=\frac{AE}{EC}=\frac{2}{5}.2=\frac{4}{5}\)
b)\(\text{Ta có:}\)
\(\frac{AE}{EC}=\frac{4}{5}\Rightarrow\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{AC}{9}=\frac{18}{9}=2\)
\(\Rightarrow AE=8cm,EC=10cm\)
bn ơi bài 1 ý a) chỉ có thể tính tỉ lệ thôi ko tính đc ra số hẳn đâu
