Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét \(\Delta ACD\) và \(\Delta ACB\) có ;
\(AD=AB;\widehat{CAD}=\widehat{CAB}=90^o;AC:chung\)
\(\Rightarrow\) \(\Delta ACD\) = \(\Delta ACB\left(cgc\right)\)
c) Xét \(\Delta DME\) và \(\Delta CMB\) có :
\(\widehat{EDM}=\widehat{DCB}\left(slt\right);DM=CM;\widehat{DME}=\widehat{CMB}\) (đối đỉnh )
\(\Rightarrow\) \(\Delta DME\) = \(\Delta CMB\) ( gcg )
\(\Rightarrow DE=CB\)
mà BC = CD ( vì \(\Delta ACD\) = \(\Delta ACB\left(cgc\right)\) )
\(\Rightarrow\) DE = CD \(\Rightarrow\) \(\Delta DEC\) cân tại D
2. a) Xét \(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=5^2-3^2\)
\(\Rightarrow AC=4cm\)

a: BC=căn 5^2+12^2=13cm
b: AB<AC<BC
=>góc C<góc B<góc A
c: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
d: góc EAC=góc ACB
góc ACB=góc ECA
=>góc EAC=góc ECA
=>ΔEAC cân tại E

xét tam giác abc vuông tại a có
a) bc2=ac2+ab2=122+52=132
bc=13
b)xét tam giác abc vá tam giac adc có
ab=ad
góc bac= góc dac
ac là cạnh chung
=>tam giác abc =tam giác adc (c.g.c)
c)
Cho tam giác ABC vuông tại A với AB = 3cm, BC= 5cm
a) tính độ dài đoạn thẳng AC
b) trên tia đối của tia AB, lấy điểm D sao cho AB = AD. Chứng minh tam giác ABC = tam giác ADC, từ đó suy ra tam giác BCD cân

a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC

a) Áp dụng định lý Py-ta-go cho \(\Delta\)vuông ABC có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=13\left(cm\right)\)
b) Xét \(\Delta ABC\)và \(\Delta ADC\)có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\gócBAC=gócDAC\left(=90^0\right)\\AC:chung\end{cases}}\)
\(\Rightarrow\Delta ABC=\Delta ADC\left(c.g.c\right)-\left(đpcm\right)\)
c) Xét \(\Delta BDC\)có: \(\hept{\begin{cases}\text{A là trung điểm BD}\\AE//BC\left(gt\right)\end{cases}}\)
\(\Rightarrow\text{E là trung điểm CD}\left(t/c\right)\)
Xét \(\Delta ADC\)vuông tại A có AE là đường trung tuyến ứng cạnh DC
\(\Rightarrow AE=\frac{1}{2}CD\left(t/c\right)=EC\left(\text{E là trung điểm CD}\right)\)
\(\Rightarrow\Delta AEC\)cân tại E (đpcm)
d) Gọi giao của AC và BE là O
Xét \(\Delta DBC\)có:\(\hept{\begin{cases}\text{BE là đường trung tuyến ứng cạnh CD }\left(gt\right)\\\text{CA là đường trung tuyến ứng cạnh BD }\left(gt\right)\end{cases}}\)
\(\Rightarrow\)O là trọng tâm của \(\Delta DBC\)
Mà DF là đường trung tuyến ứng cạnh BC
\(\Rightarrow\)CA, DF, BE cùng đồng quy tại 1 điểm (đpcm)

a) Áp dụng định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\left(cm\right)\)
\(\Rightarrow BC=\sqrt{169}=13\left(cm\right)\)
b) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\left(2\text{ góc tương ứng}\right)\)
Vì BC // AE (gt)
\(\Rightarrow\widehat{CED}=\widehat{C_1}\left(\text{so le}\right)\)
\(\Rightarrow\Delta EAC\text{ là tam giác cân. }\)
=> ĐPCM
d) Ta có: BF = CF (F là trung điểm của BC)
AB = AD (gt)
=> DP và AB là 2 đường trung tuyến của tam giác BDC
=> G là trọng điểm của tam giác BDC
=> BG là đường trung tuyến còn lại của tam giác BDC
<=> CA; DF; BE cùng đi qua 1 điểm hoặc CA; DF; BE đồng quy tại 1 điểm
=> ĐPCM
P/s: Mk vẽ hình hơi xấu, mong bn thông cảm

Á dụng định lý yTaGo vào tam giác vuông ABC ta có
BC2=AC2+AB2
BC2=122+52
BC2=169
Ý b
Xét tam giác ABC và tam giác ADC
góc CAB= góc CAD
AC chung
AB=AD
Vậy tam giác ABC= tam giác ADC(c.g.c)
ý c
Vì tam giác ABC= tam giác ADC(cmt)
suy ra góc ACD= góc ACB
mà AE song song với BC
suy ra góc EAC= góc ACB(hai góc sole trong)
mà góc ACD= góc ACB
vậy tam giác RAC cân tại E
ý d
gọi gia điểm của DF,CA,BE là I
Có FB=FC(F là trung điểm của BC)
AB=AD (gt)
suy ra DF và AC là hai đường trung tuyến của tam giác BDC
mà hai đường này cắt nhau tại I
suy ra I là trọng tâm của tam giác BDC
suy ra BE là đường trung tuyến còn lại
Vậy DF,CA,BE đồng quy tại 1 điểm

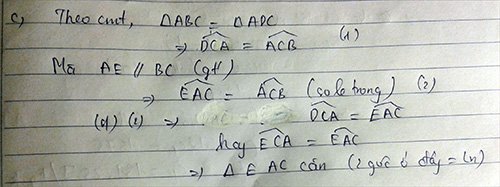
a: BC=13cm
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đo: ΔABC=ΔADC
c: Xét ΔCDB có
A là trung điểm của bD
AE//CB
Do đó: E là trung điểm của CD
Ta có: ΔCAD vuông tại A
mà AE là đường trung tuyến
nên EA=EC
hay ΔEAC cântại E
d: Gọi giao điểm của BE và AC là G
=>G là trọng tâm của ΔCDB
\(BE+AC=\dfrac{3}{2}BG+\dfrac{3}{2}CG=\dfrac{3}{2}\left(BG+CG\right)>\dfrac{3}{2}BC\)