Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!

A B C H K a,\(\Delta ABC\) cân tại A => \(\widehat{B}=\widehat{C}\)
Xét \(\Delta ABM\) và \(\Delta ACM\) có :
AB=AC (gt)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
BM=MC(gt)
Suy ra: \(\Delta ABM\) = \(\Delta ACM\)(c.g.c)
b,Xét \(\Delta\)HMB và \(\Delta\)KMC có:
\(\widehat{H}=\widehat{K}\left(=90^o\right)\)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
BM=MC(gt)
Suy ra : \(\Delta\)HMB = \(\Delta\)KMC(ch-gn)
=>BH = CK (2 cạnh tương ứng)

A B C H K P M
a) xét △ABM và △ ACM có
AB=AC ( △ABC cân tại A)
\(\widehat{B}=\widehat{C}\)( △ABC cân tại A)
BM=MC (gt)
=> △ABM = △ ACM (c.g.c)(đpcm)
b) xét △HBM và △ HCM có
\(\widehat{H}=\widehat{K}\left(=90^0\right)\)
BM=MC
\(\widehat{B}=\widehat{C}\) ( △ABC cân tại A)
=> △HBM = △ HCM (ch-gn)
=> HB=HC (2 cạnh tương ứng ) (đpcm)
c) +vì △HBM = △ HCM ( theo b)
=> \(\widehat{HMB}=\widehat{KMC}\)(2 góc tương ứng )
VÌ + BP ⊥ AC (gt)
+ MK ⊥ AC (gt)
=> BP // MK (qh từ vuông góc đến // )
=> \(\widehat{BIM}=\widehat{KIM}\) (slt)
ta có
\(\widehat{BIM}+\widehat{HMB}+\widehat{IBM}=180^0\)(đl tổng 3 góc trong △)
\(\widehat{HMB}+\widehat{IMK}+\widehat{KMC}=180^0\)(kề bù )
MÀ \(\widehat{HMB}\) chung
\(\widehat{BIM}=\widehat{IMK}\left(cmt\right)\)
=> \(\widehat{IBM}=\widehat{KMC}\)
MÀ \(\widehat{KMC}=\widehat{IMB}\) (cmt)
=> \(\widehat{IBM}=\widehat{IMB}\)
=> △ IBM cân tại I (đpcm)

Tự vẽ hình
a) Xét \(\Delta\) MHB và \(\Delta\) MKC có :
HM = HK ( gt )
\(\widehat{HMB}=\widehat{KMC}\) ( đối đỉnh )
BM = MC ( M là trung điểm của BC )
=> \(\Delta\) MHB = \(\Delta\) MKC ( c-g-c)
b) Nối HC
Vì MH \(\perp\) AB
AC \(\perp\) AB
=> MH // AC
=> \(\widehat{CHK}=\widehat{HCA}\) ( so le trong )
Theo câu a : \(\Delta\) MHB = \(\Delta\) MKC
=> \(\widehat{BHM}=\widehat{MKC}\)
Mà \(\widehat{BHM}=90^0\) ( do MH \(\perp\) BH )
=> \(\widehat{MKC}=90^0\)
=> HK \(\perp\) KC
Xét \(\Delta\) HCK vuông tại K và \(\Delta\) CHA vuông tại A có :
HC chung
\(\widehat{CHK}=\widehat{HCA}\) ( chứng minh trên )
=> \(\Delta\) HCK = \(\Delta\) CHA ( ch - gn )
=> HK = AC ( cặp cạnh tương ứng )
(tự vẽ hình nhá bạn)
a.CM:ΔMHB =ΔMKC
xét ΔMHB và ΔMKC có:
MB = MK (gt)
góc BMH = góc CMK ( hai góc đối đỉnh)
MH = MK ( gt)
=> ΔMHB =ΔMKC (c.g.c)
**hì, sorry bạn, 2 câu kia có gì chỉ sau nhé!![]()
![]()


a) Vì góc BHC = góc KMH = 90 độ
=> MK // AC
Nên góc C = góc KMB, mà góc C = góc B => góc B= góc KMB
Xét :ΔBKM và ΔMDB ta có
+ góc DBM=góc KMB ( vừa chứng minh )
+ BM là cạnh chung
=> ΔBKM=ΔMDB ( ch-gn )
b) Vì góc KHE= góc MEH = 90 độ
=> ME//BH
nên góc KHM= góc EMH (cặp góc so le trong)
Xét: ΔKHM và ΔEHM ta có
+ góc KHM = góc EMH ( vừa chứng minh )
+ MH là cạnh chung
=> ΔKHM=ΔEHM (ch-gn )
c) vì ΔBKM=ΔMDB => DM=BK
ΔKHM=ΔEHM => KH=ME
ta có DM + ME = BK + KH
=> DM + ME = BH
chúc bạn học tốt. nhớ tick cho mk nha

A B C H N M K
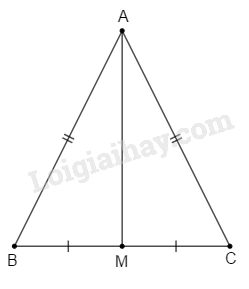
a) Xét \(\Delta AMB\) và \(\Delta AMC\) có :
AM :chung
AB = AC (tam giác ABC cân)
BM = CM (M là trung điểm của BC)
=>\(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
=>\(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
=>\(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=> \(AM\perp BC\)
b)Xét \(\Delta BHM\) và \(\Delta CKM\) có :
\(\widehat{MHB}=\widehat{MKC}=90^0\)
BM=CM (CM trên)
\(\widehat{MBH}=\widehat{MCK}\) (tam giac ABC cân)
=> \(\Delta BHM\)=\(\Delta CKM\) (cạch huyền -góc nhọn)
=>BH = CK (2 cạch tương ứng)
c)

