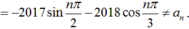Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_n=\dfrac{an^2-1}{n^2+3}\)
\(=\dfrac{an^2+3a-3a-1}{n^2+3}\)
\(=a+\dfrac{-3a-1}{n^2+3}\)
Để dãy này là dãy tăng thì \(U_{n+1}>U_n\)
=>\(a+\dfrac{-3a-1}{\left(n+1\right)^2+3}>a+\dfrac{-3a-1}{n^2+3}\)
=>\(\dfrac{-3a-1}{\left(n+1\right)^2+3}>\dfrac{-3a-1}{n^2+3}\)
=>\(\dfrac{3a+1}{\left(n+1\right)^2+3}< \dfrac{3a+1}{n^2+3}\)(1)
TH1: 3a+1>0
=>a>-1/3
(1)=>\(\dfrac{1}{\left(n+1\right)^2+3}< \dfrac{1}{n^2+3}\)
=>\(\left(n+1\right)^2+3>n^2+3\)
=>\(\left(n+1\right)^2>n^2\)
=>\(n^2+2n+1-n^2>0\)
=>\(2n+1>0\)(luôn đúng với mọi n>=1)
TH2: 3a+1<0
=>a<-1/3
(2) trở thành \(\dfrac{1}{\left(n+1\right)^2+3}>\dfrac{1}{n^2+3}\)
=>\(\left(n+1\right)^2+3< n^2+3\)
=>\(n^2+2n+1-n^2< 0\)
=>2n+1<0
=>2n<-1
=>\(n< -\dfrac{1}{2}\)(loại)
Vậy: \(a>-\dfrac{1}{3}\)

văn minh là chết b hay j mà ăn nói tục tĩu thế, dc ăn học đàng hoàng mà sao cái nết ko đàng hoàng tí nào v
trl dc thì ghi còn ko thì thôi, ai mượn phải ghi những từ ngữ tục tĩu thế
đúng tick nha ấn vào đọc tiếp trong câu trả lời trên của mình

Chọn B.
Phương pháp:
Cách giải: Ta có:
x n + 1 = x n 2 ( 2 n + 1 ) x n + 1
⇔ 1 x n + 1 = 2 ( 2 n + 1 ) + 1 x n
Đặt u n = 1 x n
ta có: u n + 1 = 2 ( 2 n + 1 ) + u n
Vậy u 100 = 2 ( 2 . 99 + 1 ) + 2 ( 2 . 98 + 1 ) + . . . 2 ( 2 . 1 + 1 ) + 3 2
⇒ = 39999 2
Vậy x 100 = 39999 2

\(\Leftrightarrow n\left(a_{n+2}-a_{n+1}\right)=\left(n+1\right)\left(a_{n+1}-a_n\right)+3n\left(n+1\right)\)
\(\Leftrightarrow\dfrac{a_{n+2}-a_{n+1}}{n+1}=\dfrac{a_{n+1}-a_n}{n}+3\)
Đặt \(\dfrac{a_{n+1}-a_n}{n}=b_n\Rightarrow\left\{{}\begin{matrix}b_1=\dfrac{a_2-a_1}{1}=-6\\b_{n+1}=b_n+3\end{matrix}\right.\)
\(\Rightarrow b_n\) là cấp số cộng với công sai 3
\(\Rightarrow b_n=b_1+\left(n-1\right)d=-6+3\left(n-1\right)=3n-9\)
\(\Rightarrow a_{n+1}-a_n=n\left(3n-9\right)=3n^2-9n\)
\(\Rightarrow a_{n+1}-\left(n+1\right)^3+6\left(n+1\right)^2-5\left(n+1\right)=a_n-n^3+6n^2-5n\)
Đặt \(a_n-n^3+6n^2-5n=c_n\Rightarrow\left\{{}\begin{matrix}c_1=6-1+6-5=6\\c_{n+1}=c_n=...=c_1=6\end{matrix}\right.\)
\(\Rightarrow a_n=n^3-6n^2+5n+6\)
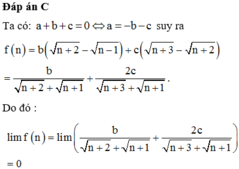

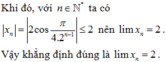
Chọn C.
Kiểm tra từng phương án đến khi tìm được đáp án đúng.
+ Ta có
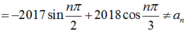
+ Ta có
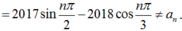
+ Ta có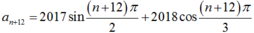
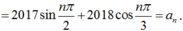
+ Ta có