Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//IK và DE=IK

A B C D E G F I K
a. Xét \(\Delta ABC\)
Ta có \(\hept{\begin{cases}AE=EB\\AD=DC\end{cases}\Rightarrow DE}\)là đường trung bình của tam giác ABC
\(\Rightarrow\)DE song song BC và \(DE=\frac{1}{2}BC\left(1\right)\)
Xét \(\Delta BGC\)có \(\hept{\begin{cases}BI=IG\\CK=KG\end{cases}\Rightarrow IK}\)là đường trung bình của tam giác BGC
\(\Rightarrow\)IK song song BC và \(IK=\frac{1}{2}BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow DE\)song song \(IK\)và \(DE=IK\)
b. Theo tính chất của trọng tâm ta có
\(GF=\frac{1}{3}AF\);\(AG=\frac{2}{3}AF\left(3\right)\)
Xét \(\Delta ABG\)có IE là đường trung bình suy ra \(IE=\frac{1}{2}AG\left(4\right)\)
Từ (3) và (4) \(\Rightarrow IE=\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AF=\frac{1}{3}AF=GF\)
Vậy \(IE=GF\)

ABCDEGHK
Ta có \(\hept{\begin{cases}GH=GD=\frac{1}{3}BD\\GE=GK=\frac{1}{3}CE\end{cases}}\)(theo tính chất của trọng tâm )
\(\Rightarrow HEDK\)là hình bình hành
a. \(\Rightarrow\)ED song song HK , ED=HK
B.\(\Rightarrow\)EH song song DK , EH=DK

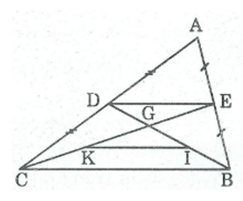
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau tại G gọi I và K theo thứ tự là trung điểm của GB GC
a tứ giác BIKC lF hình gì ? Vì sao?
b tú giác EDKI là hình gì ? Vì sao?

* Trong ΔABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ΔABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ΔGBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ΔGBC⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra:MN//BC và \(MN=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra DE//MN và DE=MN
b:Xét ΔEBC và ΔDCB có
EB=DC
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ECB}=\widehat{DBC}\)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
Suy ra: GB=GC
Suy ra: G nằm trên đường trung trực của BC(3)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(4)
Từ (3) và (4) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC

A B C D E G M N
a. Theo bài ra ta có DE và MN lần lượt là đường trung bình của tam giác ABC và GBC.
Suy ra: DE // BC; DE = 1/2 BC; MN // BC; MN = 1/2 BC
⇒ MN = DE và MN // DE.
b. Tương tự câu a ta cũng có Em và DN lần lượt là đường trung bình của tam giác BGA và tâm giác CGA. => ĐPCM